La lune est un satellite de notre terre, vers laquelle elle se dirige toujours dans son mouvement comme vers un centre, et dans le voisinage de laquelle elle se trouve constamment, de façon que si on la voyait du soleil, elle ne paraitrait jamais s'éloigner de nous d'un angle plus grand que dix minutes.
La principale différence que l'on aperçoit entre les mouvements des autres planètes et celui de la lune se peut aisément concevoir : car puisque toutes ces planètes tournent autour du soleil qui est à peu près au centre de leur mouvement, et puisqu'il les attire, pour ainsi dire, à chaque instant, il arrive delà qu'elles sont toujours à peu près à la même distance du soleil, au-lieu qu'elles s'approchent quelquefois considérablement de la terre, et d'autres fois s'en éloignent considérablement. Mais il n'en est pas tout à fait de même de la lune, on doit la regarder comme un corps terrestre. Ainsi selon les lois de la gravitation elle ne peut guère s'éloigner de nous, mais elle est retenue à peu près dans tous les temps à la même distance.

Il est si visible que la lune tourne autour de la terre, que nous ne voyons point qu'aucun philosophe de l'antiquité, ni même de ces derniers temps, ait pensé à faire un système différent. Il était réservé au P. D. Jacques Alexandre, bénédictin, de soutenir le premier que ce n'est point la lune qui tourne autour de la terre, mais la terre autour de la lune. Il a avancé cette opinion dans une dissertation sur le flux et reflux de la mer, qui remporta le prix de l'académie de Bordeaux en 1727 ; et toute son explication du flux et reflux porte sur l'hypothèse du mouvement de la terre autour de la lune. L'académie de Bordeaux, dans le programme qu'elle a fait imprimer à la tête de cet ouvrage, a eu grand soin d'avertir qu'en couronnant l'auteur, elle n'avait pas prétendu adopter son système, et que si elle n'adjugeait le prix qu'à des systèmes démontrés, elle aurait souvent le déplaisir de ne pouvoir le distribuer ; M. de Mairan, membre de cette académie et de plusieurs autres, a cru qu'il était nécessaire de réfuter l'opinion de D. Jacques Alexandre, et il l'a fait par une dissertation imprimée dans les mémoires de l'académie des Sciences de Paris 1727. Il y démontre par des observations astronomiques que la lune tourne autour de la terre, et non la terre autour de la lune. Ceux qui voudront voir ces preuves en détail, peuvent consulter la dissertation dont nous parlons, ou l'extrait qu'en a donné M. de Fontenelle.
De même que toutes les planètes premières se meuvent autour du soleil, de même la lune se meut autour de la terre ; son orbite est à peu près une ellipse dans laquelle elle est retenue par la force de la gravité ; elle fait sa révolution autour de nous en 27 jours, 7 heures 43 minutes, ce qui est aussi le temps précis de sa rotation autour de son axe. Voyez LIBRATION.
La moyenne distance de la lune à la terre est d'environ 60 1/2 diamètres de la terre, ce qui fait environ 80000 lieues.
L'excentricité moyenne de son orbite est environ 51/1000 de sa moyenne distance, ce qui produit une variation dans la distance de cette planète à la terre, car elle s'en approche et s'en éloigne alternativement de plus d'un dixième de sa moyenne distance.
Le diamètre de la lune est à celui de la terre à peu près comme 11 est à 40, c'est-à-dire, qu'il est d'environ 725 lieues, son diamètre apparent moyen est de 31'.16"1/2. et celui du soleil de 32'.12". Voyez DIAMETRE.
La surface de la lune contient environ 1555555 lieues carrées, etc. La densité de la lune est à celle de la terre, suivant M. Newton, :: 48911.39214, et à celle du soleil :: 48211 à 10000: sa quantité de matière est à celle de la terre à peu près :: 1.39, et la force de gravité sur sa surface, est à la force de gravité sur la surface de la terre :: 139:407. Voyez DENSITE, GRAVITE.
Les Astronomes sont assez d'accord entr'eux sur la plupart de ces rapports, qui sont assez exactement déterminés par les observations. Celui qui jusqu'à présent est le plus incertain, est le rapport de la densité de la lune à celle de la terre ou du soleil ; le rapport que nous venons d'en donner, est celui qu'a assigné M. Newton. Mais les observations et les calculs desquels il la déduit ne paraissent pas satisfaisants à M. Bernoulli dans sa pièce sur le flux et reflux de la mer. Il est certain que la détermination de la densité de la lune est un des problèmes les plus difficiles de l'Astronomie ; nous en parlerons à la fin de cet article, lorsque nous ferons mention des travaux des géomètres modernes sur la lune.
Phénomènes de la lune. On distingue un grand nombre de différentes apparences ou phases de la lune : tantôt elle croit, tantôt elle décroit ; quelquefois elle est cornue, d'autres fois demi-circulaire, d'autres fois bossue, pleine, et circulaire, ou plutôt sphérique. Voyez PHASE.
Quelquefois elle nous éclaire la nuit entière, quelquefois une partie de la nuit seulement ; quelquefois elle est visible dans l'hémisphère méridional, et quelquefois dans le boréal ; or comme toutes ses variations ont été d'abord découvertes par Endimion ancien grec, qui a été le premier attentif à observer les mouvements de la lune, la fable a supposé par cette raison qu'il en était amoureux.
La cause de la plupart de ces apparences, c'est que la lune est un corps obscur, opaque et sphérique, et qu'elle ne brille que de la lumière qu'elle reçoit du soleil ; ce qui fait qu'il n'y a que celle des deux moitiés qui est tournée vers cet astre, qui soit éclairée, la moitié opposée conservant toujours son obscurité naturelle.
La face de la lune qui est visible pour nous, c'est cette partie de son corps qui est tout-à-la-fais tournée vers la terre et éclairée du soleil, d'où il arrive que suivant les différentes positions de la lune par rapport au soleil et à la terre, on en voit une plus ou moins grande partie éclairée, parce que c'est tantôt une plus grande portion, & tantôt une plus petite de son hémisphère lumineux qui nous est visible.
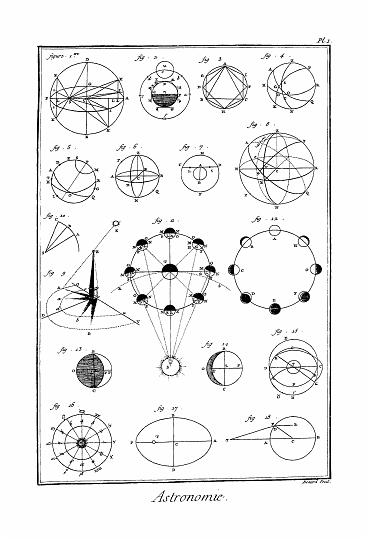
Phases de la lune. Pour concevoir les phases de la lune, supposons que S (Pl. d'Astronomie fig. 11.) représente le soleil, T la terre, R T S une portion de l'orbite de la terre, et A B C D E F l'orbite de la lune, où elle fait sa révolution autour de la terre dans l'espace d'un mois, et d'occident en orient ; joignez les centres du soleil et de la lune par la droite S L, et imaginez un plan M L N, qui passe par le centre de la lune et qui soit perpendiculaire à la droite S L, la section de ce plan avec la surface de la lune marquera la ligne qui termine la lumière et l'ombre, et qui sépare la face lumineuse de l'obscure.
Joignez les centres de la terre et de la lune par la ligne T L, à laquelle vous menerez par le centre de la lune un plan perpendiculaire P L O, ce plan donnera sur la surface de la lune le cercle qui sépare l'hémisphère visible, ou celui qui est tourné vers nous, de l'hémisphère invisible, cercle que l'on nomme par cette raison, cercle de vision.
Il s'ensuit de-là que la lune étant en A, le cercle qui termine la lumière et l'ombre, et le cercle de vision coïncideront ; de façon que toute la surface lumineuse de la lune sera tournée alors vers la terre ; la lune en ce cas sera pleine par rapport à nous, et luira toute la nuit ; mais par rapport au soleil elle sera en opposition, parce que le soleil et la lune seront vus de la terre dans des points des cieux directement opposés, l'un de ces astres se levant quand l'autre se couchera. Voyez OPPOSITION.
Quand la lune arrive en B, le disque éclairé M P N ne sera pas tourné en entier vers la terre, de façon que la partie qui sera alors tout-à-la-fais éclairée et visible, ne sera pas tout à fait un cercle, et la lune paraitra bossue comme en B. Voyez BOSSUE.
Quand elle sera arrivée vers C, où l'angle C T S est droit, il n'y aura plus qu'environ la moitié du disque éclairé qui sera tournée vers la terre, et nous verrons une demi-lune, elle sera dite alors dichotomisée, ce qui veut dire coupée en deux. Voyez DICHOTOMIE.
Dans cette situation le soleil et la lune ne sont éloignés l'un de l'autre que d'un quart de cercle, et on dit que la lune est dans son aspect quadral, ou dans sa quadrature. Voyez QUADRATURE.
La lune arrivant en D, il n'y aura plus qu'une petite partie du disque éclairé M P N qui soit tournée vers la terre, ce qui fera que la petite partie qui nous luira paraitra cornue, ou comme une faulx, c'est-à-dire terminée par de petits angles ou cornes comme en O. Voyez CORNES et FAULX.
Enfin la lune arrivant en E, elle ne montre plus à la terre aucune partie de sa face éclairée comme en O, et c'est cette position qu'on appelle nouvelle lune ; la lune est dite alors en conjonction avec le soleil, parce que ces deux astres répondent à un même point de l'écliptique. Voyez CONJONCTION.
A mesure que la lune avance vers F elle reprend ses cornes, mais avec cette différence qu'avant la nouvelle lune les cornes étaient tournées vers l'occident, au-lieu qu'à présent elles changent de position et elles regardent l'orient : lorsqu'elle est arrivée en G, elle se trouve de nouveau dichotomisée ; en H elle est encore bossue, et en A elle redevient pleine. Voyez la Figure 12.

L'angle S T L compris entre les lignes tirées des centres du soleil et de la lune, à celui de la terre, est nommée l'élongation de la lune au soleil, et l'arc P N, qui représente la portion du cercle éclairée M O N, laquelle est tournée vers nous, est par-tout presque semblable à l'arc d'élongation E L ; ou ce qui est la même chose, l'angle S T L est presque égal à l'angle M L O, selon que les Géomètres le démontrent.
Moyen de décrire les phases de la lune pour un temps donné. Que le cercle C O B P (fig. 13. et 14.) représente le disque de la lune qui est tourné vers la terre, et soit O P la ligne dans laquelle le demi-cercle O C P est projeté, laquelle nous supposerons coupée à angles droits par le diamètre B C ; prenez L P pour rayon, et dans cette supposition L F pour cosinus de l'élongation de la lune sur B C prise pour grand axe, et L F prise pour petit axe ; décrivez une ellipse B F C, cette ellipse retranchera du disque de la lune la portion B F C P de la face éclairée laquelle est visible.
Ceux qui voudront avoir la démonstration de cette pratique, la trouveront dans l'Introductio ad veram Astronomiam de Keill, qui a été traduite en français par M. Lemonnier, avec beaucoup d'additions : c'est dans le chapitre ix. de cet ouvrage que cet auteur a donné la démonstration dont nous parlons.
Comme la lune éclaire la terre d'une lumière qu'elle reçoit du soleil, de même elle est éclairée par la terre qui lui renvoye aussi de son côté par reflexion des rayons du soleil, et cela en plus grande abondance qu'elle n'en reçoit elle-même de la lune ; car la surface de la terre est environ quinze fois plus grande que celle de la lune, et par conséquent en supposant à chacune de ces surfaces une texture semblable, eu égard à l'aptitude de réflechir les rayons de lumière, la terre enverra à la lune dans cette supposition quinze fois plus de lumière qu'elle n'en reçoit d'elle. Or dans les nouvelles lunes, le côté éclairé de la terre est tourné en plein vers la lune, et il éclaire par conséquent alors la partie obscure de la lune : les habitants de la lune, s'il y en a, doivent donc avoir alors pleine terre, comme dans une position semblable nous avons pleine lune ; de-là cette lumière faible qu'on observe dans les nouvelles lunes, qui outre les cornes brillantes, nous fait apercevoir encore le reste de son disque, et nous le fait même apercevoir assez bien pour y distinguer des taches. Il est vrai que cette lumière est bien moins vive que celle du croissant, mais elle n'en est pas moins réelle ; la preuve qu'on en peut donner, c'est qu'elle Ve en s'affoiblissant à mesure que la terre s'écarte du lieu qu'elle occupait relativement au soleil et à la lune, c'est-à-dire à mesure que la lune s'approche de ses quadratures et de son opposition au soleil.
Quand la lune parvient en opposition avec le soleil, la terre vue de la lune doit paraitre alors en conjonction avec lui, et son côté obscur doit être tourné vers la lune ; dans cette position la terre doit cesser d'être visible aux habitants de la lune, comme la lune cesse de l'être pour nous lorsqu'elle est nouvelle dans sa conjonction avec le soleil ; peu après les habitants de la lune doivent voir la terre cornue, en un mot la terre doit présenter à la lune les mêmes phases que la lune présente à la terre.
Le docteur Hook cherchant la raison pourquoi la lumière de la lune ne produit point de chaleur sensible, observe que la quantité de lumière qui tombe sur l'hémisphère de la pleine lune est dispersée avant que d'arriver jusqu'à nous, dans une sphère 188 fois plus grande en diamètre que la lune, que par conséquent la lumière de la lune est 104368 plus faible que celle du soleil, et qu'ainsi il faudrait qu'il y eut tout-à-la-fais dans les cieux 104368 pleines lunes, pour donner une lumière et une chaleur égale à celle du soleil à midi. Voyez SOLEIL, CHALEUR, etc.
On a même observé que la lumière de la lune ramassée au foyer d'un miroir ardent ne produisait aucune chaleur. Sans avoir recours au calcul du docteur Hook, on peut en apporter une raison fort simple, savoir que la surface de la lune absorbe la plus grande partie des rayons du soleil, et ne nous en envoie que la plus petite partie.
Cours et mouvements de la lune. Quoique la lune finisse son cours en 27 jours 7 heures, intervalle que nous appelons mois périodiques, elle emploie cependant plus de temps à passer d'une conjonction à la suivante, et ce dernier intervalle de temps s'appelle mois synodique ou lunaison. Voyez MOIS et LUNAISON.
La raison en est que pendant que la lune fait sa révolution autour de la terre dans son orbe, la terre avec tout son système fait de son côté une partie de sa révolution autour du soleil, de façon qu'elle et son satellite, la lune, avancent l'un et l'autre de presque un signe entier vers l'orient ; le point de l'orbite, qui dans sa première position répondait à la droite qui passe par les centres de la terre et du soleil, se trouve donc alors à l'occident du soleil, et par conséquent lorsque la lune revient à ce même point elle ne doit plus se retrouver comme auparavant en conjonction avec le soleil, ce qui fait que la lunaison ne peut s'achever en moins de 29 jours et demi. Voyez PERIODIQUE, SYNODIQUE, etc.
C'est pourquoi le mouvement dont la lune s'éloigne chaque jour du soleil n'est que de 12d. et quelques minutes : on a nommé ce mouvement, le mouvement diurne de la lune au soleil.
Si le plan de l'orbite de la lune était coincident avec celui de l'écliptique, c'est-à-dire si la terre et la lune se mouvaient dans un même plan, le chemin de la lune dans les cieux, Ve de la terre, paraitrait précisément le même que celui du soleil, avec cette seule différence que le soleil se trouverait décrire son cercle dans l'espace d'une année, et que la lune décrirait le sien dans un mois ; mais il n'en est pas ainsi, car ces deux plans se coupent l'un l'autre dans une droite qui passe par le centre de la terre, et sont inclinés l'un à l'autre d'un angle d'environ 5d. Voyez INCLINAISON.
Supposons, par exemple, que A B (fig. 15.) soit une portion de l'orbite de la terre, T la terre, et C E D F l'orbite de la lune dans lequel se trouve le centre de la terre ; décrivez de ce même centre T, dans le plan de l'écliptique, un autre cercle C G D H dont le demi-diamètre, soit égal à celui du demi-diamètre de l'orbite de la lune, ces deux cercles qui sont dans un différent plan et qui ont le même centre T, se couperont l'un l'autre dans une droite D C qui passera par le centre de la terre, et par conséquent l'une des moitiés C E D de l'orbite de la lune sera élevée au-dessus du plan du cercle C G H vers le nord, et l'autre moitié D F C sera au-dessous vers le sud. La droite D C dans laquelle les deux cercles se coupent, s'appelle la ligne des nœuds, et les points des angles C et D les nœuds, celui de ces nœuds dans lequel la lune s'élève au-dessus du plan de l'écliptique vers le nord, s'appelle nœud ascendant ou tête du dragon, et l'autre nœud descendant et queue du dragon. Voyez NOEUD ; et l'intervalle de temps que la lune emploie en partant du nœud ascendant pour revenir au même nœud, s'appelle mois dracontique. Voyez DRAGON et DRACONTIQUE.

Si la ligne des nœuds était immobile, c'est-à-dire si elle n'avait d'autre mouvement que celui par lequel elle tourne autour du soleil, elle regarderait toujours en ce cas le même point de l'écliptique, c'est-à-dire qu'elle resterait toujours parallèle à elle-même. Mais ces observations prouvent au contraire que la ligne des nœuds change continuellement de place, que sa situation décline toujours de l'orient à l'occident contre l'ordre des signes, et qu'elle finit la révolution de ce mouvement rétrograde dans un espace d'environ 19 ans, après quoi, chacun des nœuds revient au même point de l'écliptique dont il s'était d'abord éloigné. Voyez CYCLE.
Il s'ensuit de-là que la lune n'est jamais précisément dans l'écliptique que deux fois dans chaque période, savoir lorsqu'elle se trouve dans ses nœuds. Dans tout le reste de son cours elle s'éloigne plus ou moins de l'écliptique, suivant qu'elle est plus ou moins proche de ces nœuds. Les points F et E où elle est le plus éloignée de ces nœuds, sont nommés ses limites. Voyez LIMITE.
La distance de la lune à l'écliptique est nommée sa latitude, et elle se mesure par un arc de cercle qui Ve de la lune perpendiculairement à l'écliptique, et qui est comprise entre la lune et l'écliptique, ayant la terre pour centre ; la latitude de la lune, même lorsqu'elle est la plus grande, comme en E et en F, ne passe jamais 5d. et environ 18'. et cette latitude est la mesure des angles des nœuds. Voyez LATITUDE.
Il parait par ces observations, que la distance de la lune à la terre change continuellement, de sorte que la lune est tantôt plus proche et tantôt plus loin de nous. En effet, elle parait tantôt sous un angle plus grand, tantôt sous un angle plus petit : l'angle sous lequel le diamètre horizontal de la lune a été observé lorsqu'elle était pleine et périgée, excède un peu 33'1/2 ; mais étant pleine et apogée, on ne l'aperçoit guère que sous un angle de 29d. 30'. la raison en est que la lune ne se meut point dans une orbite circulaire qui ait la terre pour centre, mais dans une orbite à peu près elliptique (telle que celle qui est représentée dans la fig. 17.) dont l'un des foyers est le centre de la terre ; A P y marque le grand axe de l'ellipse, ou la ligne des apsides ; T C l'excentricité : le point A qui est la plus haute apside s'appelle l'apogée de la lune, P ou l'apside inférieure est le périgée de la lune, ou le point de son orbite dans lequel elle est le plus proche de la terre. Voyez APOGEE et PERIGEE.
L'espace de temps que la lune emploie en partant de l'apogée pour revenir au même point, s'appelle mois anomalistique.
Si la ligne des apsides de la lune n'avait d'autre mouvement que celui par lequel elle est emportée autour du soleil, elle conserverait toujours une position semblable, c'est-à-dire qu'elle resterait parallèle à elle-même, qu'elle regarderait toujours le même point des cieux, et qu'on l'observerait toujours dans le même point de l'écliptique ; mais on a observé que la ligne des apsides est aussi mobile, ou qu'elle a un mouvement angulaire autour de la terre d'occident en orient selon l'ordre des signes, mouvement dont la révolution se fait dans l'espace d'environ neuf années. Voyez APSIDE.
Les irrégularités du mouvement de la lune et de celui de son orbite sont très-considérables : car
1°. quand la terre est dans son aphélie, la lune finit sa révolution dans un temps plus court ; au contraire, quand la terre est dans son périhélie, la lune ralentit alors son mouvement ; ainsi ses révolutions autour de la terre se font en moins de temps, toutes choses d'ailleurs égales, lorsque la terre est dans son aphélie que lorsqu'elle est dans son périhélie, de sorte que les mois périodiques ne sont point égaux les uns aux autres. Voyez PERIODIQUE.
2°. Quand la lune est dans ses syzygies, c'est-à-dire dans la droite qui joint les centres de la terre et du soleil, ou, ce qui est la même chose, dans sa conjonction ou son opposition, elle se meut (toutes choses égales d'ailleurs) plus vite que dans les quadratures. Voyez SYZYGIE.
3°. Le mouvement de la lune varie suivant les différentes distances de cet astre aux syzygies, c'est-à-dire à l'opposition ou à la conjonction dans le premier quartier, c'est-à-dire depuis la conjonction jusqu'à la première quadrature, elle perd un peu de sa vitesse pour la recouvrer dans le second quartier, et elle en perd encore un peu dans le troisième pour la recouvrer dans le quatrième. Ticho Brahé a découvert le premier cette inégalité, et l'a nommée variation de la lune. Voyez VARIATION.
4°. La lune se meut dans une ellipse, dont l'un des foyers est placé dans le centre de la terre, et son rayon vecteur décrit autour de ce point des aires proportionnelles au temps, comme il arrive aux planètes à l'égard du soleil ; son mouvement doit donc être plus rapide dans le périgée, et plus lent dans l'apogée.
5°. L'orbite même de la lune est variable, et ne conserve pas toujours la même figure, son excentricité augmentant quelquefois, et diminuant d'autres fais. Elle est la plus grande, lorsque la ligne des apsides coïncide avec celle des syzygies ; et la plus petite, lorsque la ligne des apsides coupe l'autre à angles droits.
Cela est aisé à reconnaître par les diamètres apparents que l'on observe. M. Picard est le premier qui ait découvert que la lune périgée au premier et au second quartier, paraissait sous un angle d'environ une minute plus petit que lorsqu'elle était pleine et périgée ; ce qui a fait connaître la loi suivant laquelle l'excentricité de l'orbite variait à chaque lunaison. Il est encore à remarquer que la différence entre la plus grande et la plus petite excentricité, est si grande, que dans le premier de ces deux cas elle excède de la moitié cette dernière. Par les observations des éclipses de lune on avait conclu autrefois la plus petite excentricité de l'orbite de cette planète ; ce qui donnait pour sa plus grande équation du centre, 5° ou 4° 59' 30"°; mais de l'observation de M. Picard il a fallu conclure que l'équation du centre pouvait être vers le premier ou second quartier de 7d 30' 0", et qu'ainsi les deux plus grandes équations qui peuvent arriver, l'une dans la pleine lune, l'autre dans les quadratures, diffèrent d'environ 2° 30'.
6°. L'apogée de la lune n'est pas exempt d'irrégularité ; car on trouve qu'il se meut en avant, lorsqu'il coïncide avec la ligne des syzygies, et en arrière, lorsqu'il coupe cette ligne à angles droits. Ces deux mouvements en avant et en arrière ne sont pas non plus égaux. Dans la conjonction ou l'opposition, le mouvement en avant est assez rapide ; dans les quadratures, ou bien l'apogée se meut lentement en avant, ou bien il s'arrête, ou bien il se meut en arrière.
7°. Le mouvement des nœuds n'est pas uniforme ; mais quand la ligne des nœuds coïncide avec celle des syzygies, les nœuds s'arrêtent. Lorsque les nœuds sont dans les quadratures, c'est-à-dire que leurs lignes coupent celles des syzygies à angles droits, ils vont en arrière d'orient en occident, et M. Newton sait voir que c'est avec une vitesse de 16" 19"' 24"" par heure.
Le seul mouvement uniforme qu'ait la lune, est celui par lequel elle tourne autour de son axe, précisément dans le même espace de temps qu'elle emploie à faire sa révolution autour de nous dans son orbite, d'où il arrive qu'elle nous présente toujours à-peu-près la même face : nous disons à-peu-près, et non pas exactement ; car comme le mouvement de la lune autour de son axe est uniforme, et que cependant son mouvement ou sa vitesse dans son orbite est inégale, il arrive de-là que quelque partie du limbe de la lune s'éloigne quelquefois du centre de son disque, et que d'autres fois elle s'en approche, et que quelques parties qui étaient auparavant invisibles, deviennent par-là visibles. Voyez VIBRATION.
Si la lune décrivait un cercle autour de la terre, et qu'elle décrivit ce cercle d'un mouvement uniforme dans le même temps qu'elle tourne autour de son axe, assurément ce serait toujours le plan du même méridien lunaire qui passerait par notre oeil ou par le centre de la terre, et l'on apercevrait exactement chaque jour le même hémisphère. Il suit de ces observations que si la lune est habitée, quelques-uns de ses habitants doivent tantôt voir la terre et tantôt ne la plus voir, que près de la moitié doivent ne la voir jamais, et près de la moitié la voir toujours. Cette espèce d'ondulation ou de vacillation de la lune se fait d'abord d'occident en orient, ensuite d'orient en occident ; de sorte que diverses régions qui paraissaient situées vers le bord occidental ou oriental de la lune, se cachent ou se montrent alternativement. On a donné à ce mouvement le nom de libration.
Cette uniformité de rotation produit encore une autre irrégularité apparente ; car l'axe de la lune n'étant point perpendiculaire au plan de son orbite, mais étant un peu incliné à ce plan, et cet axe conservant continuellement son parallelisme dans son mouvement autour de la terre, il faut nécessairement qu'il change de situation, par rapport à un observateur placé dans la terre, et à la vue duquel il présentera tantôt l'un des pôles, et tantôt l'autre. Desorte que l'observateur, placé sur la surface de la terre, ne verra pas toujours exactement un hémisphère terminé par un plan qui passe par l'axe de la lune, mais l'axe se trouvera presque toujours tantôt d'un côté de ce plan, tantôt de l'autre ; ce qui fait qu'il parait avoir une espèce d'ondulation ou vacillation.
Causes physiques du mouvement de la lune. Nous avons déjà observé que la lune se meut autour de la terre suivant les mêmes lois et de la même manière que les autres planètes se meuvent autour du soleil ; et il s'ensuit de-là que l'explication du mouvement lunaire en général retombe dans celle du mouvement des autres planètes autour du soleil. Voyez PLANETE et TERRE.
Quant aux irrégularités particulières au mouvement de la lune, et auxquelles la terre et les autres planètes ne sont point sujettes, elles proviennent du soleil qui agit sur la lune, et trouble son cours ordinaire dans son orbite, et elles peuvent toutes se déduire mécaniquement de la même loi qui dirige le mouvement général de la lune, je veux dire de la loi de gravitation et d'attraction. Voyez GRAVITATION.
Les autres planètes secondaires, par exemple les satellites de Jupiter et de Saturne sont sans doute sujets aux mêmes irrégularités que la lune, parce qu'ils sont exposés à cette même force d'action du soleil sur eux, qui peut les troubler dans leur cours ; aussi aperçoit-on dans le mouvement de ces satellites de grandes irrégularités. Voyez SATELLITE.
Astronomie de la lune. Premier moyen de déterminer la révolution de la lune autour de la terre ou le mois périodique, et le temps compris entre une opposition et la suivante ou le mois synodique.
Puisque la lune dans le milieu d'une éclipse lunaire est opposée au soleil, voyez ECLIPSE, calculez le temps compris entre deux éclipses ou oppositions, et divisez-le par le nombre des lunaisons qui se sont écoulées dans cet intervalle, le quotient sera la quantité du mois synodique. Calculez le mouvement moyen du soleil durant le temps du mois synodique, et ajourez y le cercle entier décrit par la lune, après quoi vous ferez cette proportion : comme la somme trouvée est à 360 secondes, de même la quantité du mois synodique est à celle du périodique. Ainsi Copernic ayant observé à Rome en l'an 1500, le 6 Novembre à minuit une éclipse de lune, et une autre à Cracovie le premier Aout 1523, à 4 heures 25 secondes, il en conclut de cette sorte la quantité du mois synodique de 29 jours 12 heures 41. min. 9 sec. 9 tierces.
e même auteur, au moyen de deux autres éclipses observées, l'une à Cracovie, l'autre à Babylone, a déterminé encore plus exactement la quantité du mois synodique qu'il a trouvée par-là ;
De 29 jours,.... 11 heures 43' 3" 10"'
Moyen mouvement du soleil en même temps,.. 19°6'24"18"'
Moyen de la lune,....................... 389°6'24"18"'
Quantité du mois périodique, 27 jours 7 heures 43' 5".
D'où il s'ensuit
1°. que la quantité du mois périodique étant donnée, on peut trouver par la règle de trois le mouvement diurne et horaire de la lune, etc. et de cette sorte construire des tables du moyen mouvement de la lune.
2°. Si on soustrait le moyen mouvement diurne du soleil du moyen mouvement diurne de la lune, le restant donnera le mouvement diurne de la lune au soleil ; ce qui fournira le moyen de construire une table de ce mouvement diurne.
3°. Puisqu'au milieu des éclipses totales, la lune se trouve dans le nœud ; il s'ensuit de-là que si on cherche le lieu du soleil pour ce temps, et qu'on y ajoute six signes, la somme donnera le lieu du nœud.
4°. En comparant les observations anciennes avec les modernes, il parait, comme nous l'avons déjà dit, que les nœuds ont un mouvement, et qu'ils avancent in antecedentia, ou contre l'ordre des signes, c'est-à-dire, de taurus à aries, d'aries à pisces, etc. Si l'on ajoute donc au moyen mouvement diurne de la lune le mouvement diurne des nœuds, la somme sera le mouvement de la lune par rapport aux nœuds ; et on pourra conclure de-là, au moyen de la règle de trois, en combien de temps la lune parcourt 360°, à compter du nœud ascendant, ou combien de temps elle met à revenir à ce point depuis qu'elle en est partie, c'est-à-dire la quantité du mois dracontique.
Moyen de trouver l'âge de la lune. Ajoutez au jour du mois, l'épacte de l'année, et les mois écoulés depuis Mars inclusivement, la somme, si elle est au-dessous de 30, et si elle est au-dessus, son excès sur 30 sera l'âge de la lune ; en supposant que le mois ait 31 jours, et si le mois n'a que 30 jours, sera l'excès sur 29.
La raison de cette pratique est
1°. que l'épacte de l'année donne toujours l'âge de la lune au premier Mars.
2°. Que comme l'année lunaire est plus courte de 11 à 12 jours que l'année solaire (voyez EPACTE), et que l'année a 12 mois, la nouvelle lune anticipe ou remonte à-peu-près d'un jour chaque mois, en commençant par Mars. Au reste cette pratique ne donne l'âge de la lune que d'une manière approchée ; la seule manière de connaître exactement l'âge de la lune, c'est d'avoir recours aux tables astronomiques.
Pour trouver le temps où la lune passe au méridien, on remarquera
1°. que le jour de la nouvelle lune, la lune passe au méridien en même temps que le soleil.
2°. Que d'un jour à l'autre, le passage de la lune au méridien retarde d'environ trois quarts d'heure (voyez FLUX et REFLUX), ainsi prenez autant de fois trois quarts d'heure qu'il y a de jours dans l'âge de la lune, et vous aurez le temps qui doit s'écouler entre l'heure de midi d'un jour donné, et le passage de la lune au méridien qui doit suivre. Cette seconde pratique n'est encore qu'approchée et seulement pour un usage journalier et grossier. Le véritable temps du passage de la lune au méridien, se trouve dans les tables astronomiques, dans les éphémérides, dans la connaissance des temps, etc. Voyez EPHEMERIDE, etc.
Quant aux éclipses de lune, voyez ECLIPSE ; sur la parallaxe de la lune, voyez PARALLAXE.
Théorie des mouvements et des irrégularités de la lune. Supposons qu'on demande dans un temps donné, le lieu de la lune dans le zodiaque en longitude, nous trouverons d'abord dans les tables le lieu où la lune serait, si son mouvement était uniforme, c'est ce qu'on appelle son mouvement moyen, lequel est quelquefois plus prompt, et quelquefois plus lent que le mouvement vrai. Pour trouver ensuite où elle doit se rencontrer en conséquence de son mouvement vrai, qui est aussi l'apparent, nous chercherons dans une autre table à quelle distance elle est de son apogée, car cette distance rend plus ou moins grande la différence entre le mouvement vrai et le mouvement moyen, et les deux lieux qui correspondent à ces deux mouvements. Le vrai lieu trouvé de la sorte n'est pas encore le vrai lieu, mais il en est plus ou moins éloigné, selon que la lune est plus ou moins éloignée et du soleil, et de l'apogée du soleil ; et comme cette variation dépend en même temps de ces deux différentes distances, il faudra les considérer et les combiner ensemble dans une table à part ; cette table donne la correction qu'il faut faire au vrai lieu trouvé ci-dessus. Mais ce lieu ainsi corrigé n'est pas encore le vrai lieu, à moins que la lune ne soit en conjonction ou en opposition ; si elle est hors de ces deux cas, il y aura encore une correction à faire, laquelle dépend de deux éléments qu'il faut prendre ensemble, et comparer, savoir la distance du lieu corrigé de la lune au soleil, et celle du lieu où elle est par rapport à son propre apogée, cette dernière distance ayant été changée par la dernière correction.
Par toutes ces opérations et ces corrections, on arrive enfin au vrai lieu de la lune pour l'instant donné, mais il faut convenir qu'il se rencontre en tout cela des difficultés prodigieuses. Les inégalités de lune sont si grandes que ç'a été inutilement que les Astronomes ont travaillé jusqu'au grand Newton à les soumettre à quelque règle. C'est à ce grand homme que nous devons la découverte de leur cause mécanique, ainsi que la méthode de les calculer et de les déterminer, de façon qu'on peut dire de lui qu'il a découvert un monde presque entier, ou plutôt qu'il se l'est soumis.
Suivant la théorie de M. Newton, on démontre d'une manière fort élégante les lois mécaniques d'où dépendent les mouvements que l'on a reconnus tant à l'égard de la lune que de son orbite apparent. C'est une chose remarquable que l'astre qui est le plus proche de la terre, soit celui dont les mouvements nous sont, pour ainsi dire, le moins connus. Au reste, quelque utilité que l'Astronomie ait retiré du travail de M. Newton, les mouvements de la lune sont si irréguliers, qu'on n'est pas encore parvenu à découvrir entièrement tout ce qui appartient à la théorie de cette planète, et cela faute d'une longue suite d'observations qui demandent beaucoup de veilles et d'assiduités.
M. Newton fait voir par la théorie de la gravité, que les plus grandes planètes, en tournant autour du soleil, peuvent emporter avec elles de plus petites planètes qui tournent autour d'elles, et il prouve à priori, que ces dernières doivent se mouvoir dans des ellipses dont les foyers se trouvent dans le centre des plus grandes, et qu'en même temps leur mouvement dans leur orbite est différemment troublé par l'action du soleil. Enfin, il infère de-là que les satellites de Saturne sont sujets à des irrégularités analogues. Il examine d'après la même théorie quelle est la force du soleil pour troubler le mouvement de la lune, il détermine quel serait l'incrément horaire de l'aire que la lune décrirait dans une orbite circulaire par des rayons vecteurs aboutissant à la terre, sa distance de la terre, son mouvement horaire dans une orbite circulaire et elliptique, le mouvement moyen des nœuds, le mouvement vrai des nœuds, la variation horaire de l'inclinaison de l'orbite de la lune au plan de l'écliptique.
Enfin, il a conclu de la même théorie que l'équation annuelle du mouvement moyen de la lune provient de la différente figure de son orbite, et que cette variation a pour cause la différente force du soleil ; laquelle étant plus grande dans le périgée, allonge alors l'orbite, et devenant plus petite dans l'apogée, lui permet de nouveau de se contracter. Dans l'allongement de l'orbite, la lune se meut plus lentement, et dans la contraction elle Ve plus vite, et l'équation annuelle propre à compenser cette inégalité est nulle, lorsque le soleil est apogée ou périgée ; dans la moyenne distance du soleil, elle Ve suivant les observations à 11' 50", et dans les autres distances elle est proportionnelle à l'équation du centre du soleil, on l'ajoute au moyen mouvement de la lune, lorsque la terre Ve de son aphélie au périhélie, et on la soustrait lorsqu'elle Ve en sens contraire. Or, supposant le rayon du grand orbe de mille parties et l'excentricité de la terre de 16 7/8, cette équation, lorsqu'elle sera la plus grande, ita suivant la théorie de la gravité à 11' 49"°; ce qui s'accorde, comme l'on voit, avec l'observation.
M. Newton ajoute que dans le périhélie de la terre les nœuds de la lune et son apogée se meuvent plus promptement que dans l'aphélie, et cela en raison triplée inverse de la distance de la terre au soleil, d'où proviennent des équations annuelles des mouvements des nœuds proportionnelles à celui du centre du soleil ; or les mouvements du soleil sont en raison doublée inverse de la distance de la terre au soleil, et la plus grande équation du centre que cette inégalité puisse produire est de 1° 56' 26", en supposant l'excentricité de 16 15/15 partie.
Si le mouvement du soleil était en raison triplée inverse de sa distance, cette inégalité donnerait pour plus grande équation 2° 56' 9", et par conséquent les plus grandes équations que puissent produire les inégalités des mouvements de l'apogée de la lune et des nœuds, sont à 2° 56' 9", comme le mouvement diurne de l'apogée de la lune et le moyen mouvement diurne de ces nœuds sont au moyen mouvement diurne du soleil ; d'où il s'ensuit que la plus grande équation du moyen mouvement de l'apogée est d'environ 19' 52", et que la plus grande équation du moyen mouvement des nœuds est de 9' 27". On ajoute la première équation, et on soustrait la seconde, lorsque la terre Ve de son périhélie à son aphélie, et dans l'autre cas on fait le contraire.
Il parait aussi par la même théorie de la gravité, que l'action du soleil sur la lune doit être un peu plus grande, quand l'axe transverse de l'orbite lunaire passe par le soleil, que lorsqu'il coupe à angles droits la droite qui joint la terre et le soleil, et que par conséquent l'orbite lunaire est un peu plus grande dans le premier cas que dans le second ; ce qui donne naissance à une autre équation du moyen mouvement de la lune, laquelle dépend de la situation de l'apogée de la lune par rapport au soleil, et devient la plus grande qui soit possible, lorsque l'apogée de la lune est à 45° du soleil ; et nulle, lorsque la lune arrive aux quadratures et aux syzygies. On l'ajoute au moyen mouvement, lorsque l'apogée de la lune passe des quadratures aux syzygies, et on l'en soustrait, lorsque l'apogée passe des syzygies aux quadratures.
Cette équation que M. Newton appelle semestre, devient de 3' 45", lorsqu'elle est la plus grande qui soit possible (c'est-à-dire à 45° de l'apogée) dans les moyennes distances de la terre au soleil ; mais elle augmente et diminue en raison triplée inverse de la distance du soleil ; ce qui fait que dans les plus grandes distances du soleil elle est environ de 3' 34", et dans la plus petite, de 3' 56"; mais lorsque l'apogée de la lune est hors des octants, c'est-à-dire a passé 45°, elle diminue alors, et elle est à la plus grande équation, comme le sinus de la distance double de l'apogée de la lune à la plus prochaine syzygie ou quadrature, est au rayon.
De la même théorie de la gravité il s'ensuit que l'action du soleil sur la lune, est un peu plus grande, lorsque la droite tirée par les nœuds de la lune, passe par le soleil, que lorsque cette ligne est à angles droits avec celle qui joint le soleil et la terre ; et de-là se déduit une autre équation du moyen mouvement de la lune, que M. Newton appelle seconde équation semestre, et qui devient la plus grande possible, lorsque les nœuds sont dans les octants du soleil, c'est-à-dire à 45°. du soleil ; et nulle, lorsqu'ils sont dans les syzygies ou quadratures. Dans d'autres situations des nœuds cette équation est proportionnelle au sinus du double de la distance de chaque nœud à la dernière syzygie ou quadrature. On l'ajoute au moyen mouvement de la lune, lorsque les nœuds sont dans leur passage des quadratures du soleil à la plus prochaine syzygie, et on l'en soustrait dans leur passage des syzygies aux quadratures.
Lorsqu'elle est la plus grande qu'il est possible, c'est-à-dire dans les octants et dans la distance moyenne de la terre au soleil, elle monte à 45", selon qu'il parait par la théorie de la gravité : à d'autres distances du soleil, cette équation dans les octants des nœuds est réciproquement comme le cube de la distance du soleil à la terre ; elle est par conséquent dans le périgée du soleil de 45", et dans son apogée, d'environ 49".
Suivant la même théorie de la gravité, l'apogée de la lune Ve le plus vite, lorsqu'il est ou en conjonction ou en opposition avec le soleil, et il retrograde lorsqu'il est en quadrature avec lui. L'excentricité est dans le premier cas la plus grande possible, et dans le second, la plus petite possible. Ces inégalités sont très-considérables, et elles produisent la principale équation de l'apogée qui s'appelle semestre ou semimenstruelle. La plus grande équation semimenstruelle est d'environ 12' 18", suivant les observations.
Horrox a observé le premier que la lune faisait à-peu-près sa révolution dans une ellipse dont la terre occupait le foyer ; et Halley a mis le centre de l'ellipse dans une épicycle dont le centre tourne uniformément autour de la terre, et il déduit du mouvement dans l'épicycle les inégalités qu'on observe dans le progrès et la rétrogradation de l'apogée et la quantité de l'excentricité.

Supposons la moyenne distance de la lune à la terre divisée en 100000 parties, et que T (Pl. astronom. figure 18.) représente la terre, et T C, la moyenne excentricité de la lune de 5505 parties, qu'on prolonge T C en B, de façon que B C puisse être le sinus de la plus grande équation semimenstruelle ou de 11° 18' pour le rayon T C, le cercle B D A, décrit du centre C et d'un intervalle C B, sera l'épicycle dans lequel est placé le centre de l'orbite lunaire, et dans lequel il tourne selon l'ordre des lettres B D A. Prenez l'angle B C D égal au double de l'argument annuel, ou au double de la distance du vrai lieu du soleil à l'apogée de la lune corrigée une fais, et C T D sera l'équation semimenstruelle de l'apogée de la lune, et T D, l'excentricité de son orbite, en allant vers l'apogée ; d'où il s'ensuit qu'on peut trouver par les méthodes connues le moyen mouvement de la lune, son apogée et son excentricité, comme aussi le grand axe de son orbite de 200000 parties, son vrai lieu et sa distance de la terre. On peut voir dans les Principes mathématiques les corrections que M. Newton fait à ce calcul.
Voilà la théorie de la lune telle que M. Newton nous l'a donnée dans le troisième livre de son bel ouvrage intitulé : Philosophiae naturalis principia mathematica : mais ce grand géomètre n'a point démontré la plupart des règles qu'il donne pour calculer le lieu de la lune. Dans le second volume de l'astronomie de Grégori, on trouve un autre ouvrage de M. Newton, qui a pour titre, Lunae theoria Newtoniana, et où il explique d'une manière encore plus précise et plus particulière les opérations qu'il faut faire pour trouver le lieu de la lune dans un temps donné, mais toujours sans démonstration : dans le commentaire que les PP. Le Sueur et Jacquier, Minimes, ont publié sur les principes de Newton, M. Calandrin, célèbre professeur de mathématiques à Genève, et depuis l'un des principaux magistrats de la république, a commenté fort au-long toute cette théorie, et a tâché de développer la méthode que M. Newton a suivie ou pu suivre pour y parvenir : mais il avoue que sur certains points, comme le mouvement de l'apogée et l'excentricité, il y a encore quelque chose à désirer de plus précis et de plus exact que ne donne la théorie de M. Newton. Rien ne serait plus utîle que la connaissance des mouvements de la lune pour la recherche des longitudes ; et c'est ce qui doit porter tous les Astronomes et les Géomètres à perfectionner de plus en plus les tables qui doivent y servir. Voyez LONGITUDE, et la fin de cet article.
Au reste, quelles que soient les causes des irrégularités des mouvements de la lune, les observations ont appris qu'après 223 lunaisons, c'est-à-dire 223 retours de la lune vers le soleil, les circonstances du mouvement de la lune redevenant les mêmes, par rapport au soleil et à la terre, ramènent dans son cours les mêmes irrégularités qu'on y avait observées dix-huit ans auparavant. Une suite d'observations continuées pendant une telle période avec assez d'assiduité et d'exactitude, donnera donc le mouvement de la lune pour les périodes suivantes.
Ce travail si long et si pénible d'une période entière bien remplie d'observations, fut entrepris par M. Halley, lorsqu'il était déjà dans un âge si avancé, qu'il ne se flattait plus de le pouvoir terminer. Ce grand et courageux astronome nous avertit que n'étant encore qu'à la fin d'une autre période qui ne contient que 111 lunaisons, et qui ne donne pas si exactement que celle de 223 le retour des mêmes inégalités, il pouvait déjà déterminer sur mer la longitude à 20 lieues près vers l'équateur, à 15 lieues près dans nos climats, et plus exactement encore plus près des pôles.
Mais on n'aura rien à désirer, et on aura l'ouvrage le plus utîle qu'on puisse espérer sur cette matière, si le travail qu'a entrepris M. Lemonnier s'accomplit. Depuis qu'il s'est attaché à la théorie de la lune, il a fait un si grand nombre d'excellentes observations, qu'on ne saurait espérer de voir cette partie de la période mieux remplie : et dans les institutions astronomiques qu'il a publiées en 1746, il a déjà donné d'après la théorie de M. Newton, des tables du mouvement de la lune, plus exactes et plus complete s qu'aucune de celles qu'on a publiées jusqu'ici.
A la fin de ce même ouvrage, il donne la manière de se servir de ces tables, et de calculer par leur secours quelques lieux de la lune. Nous parlerons à la fin de cet article de la suite de ses travaux par rapport à cet objet.
Nature et propriétés de la lune.
1°. De ce que la lune ne montre qu'une petite partie de son disque, lorsqu'elle suit le soleil prêt à se coucher ; de ce que cette portion croit à mesure qu'elle s'éloigne du soleil jusqu'à la distance de 180d où elle est pleine, qu'elle diminue au contraire à mesure que l'astre s'approche du soleil, et qu'elle perd toute sa lumière lorsqu'elle l'a atteint ; de ce que sa partie lumineuse est constamment tournée vers l'occident lorsqu'elle est dans son croissant, et vers l'orient quand elle est dans son décours ; de tout cela il suit évidemment qu'elle n'a d'éclairée que la seule partie sur laquelle tombent les rayons du soleil ; enfin des phénomènes des éclipses qui n'arrivent que lorsque la lune est pleine, c'est-à-dire lorsqu'elle est éloignée de 180d du soleil, on doit conclure qu'elle n'a point de lumière propre, mais qu'elle emprunte du soleil toute celle qu'elle nous envoie. Voyez PHASE, ÉCLIPSE.
2°. La lune disparait quelquefois par un ciel clair, serein, de façon qu'on ne saurait la découvrir avec les meilleurs verres, quoique des étoiles de la 5e et 6e grandeur restent toujours visibles. Kepler a observé deux fois ce phénomène en 1581 et 1583 ; et Hévelius en 1620 ; Riccioli, d'autres jésuites de Boulogne, et beaucoup d'autres personnes dans la Hollande observèrent la même chose le 14 Avril 1642, quoique cependant la lune fût restée toujours visible à Venise et à Vienne. Le 23 Décembre 1703, il y eut une autre disparition totale, la lune parut d'abord à Arles d'un brun jaunâtre, et à Avignon elle parut rougeâtre et transparente, comme si le soleil avait brillé au-travers ; à Marseille un des côtés parut rougeâtre, et l'autre fort obscur ; et à la fin, elle disparut entièrement, quoique par un temps serein. Il est évident dans ce phénomène que ces couleurs qui paraissaient différentes dans un même temps, n'appartenaient pas à la lune, mais qu'elles provenaient de quelque matière qui l'entourait et qui se trouvait différemment disposée pour donner passage à des rayons de telle ou telle couleur.
3°. L'oeil nud ou armé d'un télescope, voit dans la face de la lune des parties plus obscures que d'autres, qu'on appelle maculae ou taches. A travers le télescope, les bornes de la lumière paraissent dentelées et inégales, composées d'arcs dissemblables, convexes et concaves. On observe aussi des parties lucides, dispersées ou semées parmi de plus obscures, et on voit des parties illuminées par-delà les limites de l'illumination ; d'autres intermédiaires, restant toujours dans l'obscurité et auprès des taches, ou même dans les taches : on voit souvent de ces petites taches lumineuses. Outre les taches qu'avaient observées les anciens, il en est d'autres variables, invisibles à l'oeil nud, qu'on nomme taches nouvelles, qui sont toujours opposées au soleil, et qui se trouvent par cette raison dans les parties qui sont le plutôt éclairées dans le croissant, et qui perdent dans le décours leur lumière plus tard que les autres intermédiaires, tournant autour de la lune, et paraissant quelquefois plus grandes et quelquefois plus petites. Voyez TACHES.
Or, comme toutes les parties de la surface de la lune sont également illuminées par le soleil, puisqu'elles en sont également éloignées ; il s'ensuit delà que s'il y en a qui paraissent plus brillantes, et d'autres plus obscures, c'est qu'il en est qui réfléchissent les rayons du soleil plus abondamment que d'autres, et par conséquent qu'elles sont de différente nature : les parties qui sont le plutôt éclairées par le soleil, sont nécessairement plus élevées que les autres, c'est-à- dire qu'elles sont au-dessus du reste de la surface de la lune. Les nouvelles taches répondent parfaitement aux ombres des corps terrestres.
4°. Hévelius rapporte qu'il a souvent trouvé dans un temps très-serein, lors même que l'on pouvait voir les étoiles de la 6e et de la 7e grandeur, qu'à la même hauteur et à la même élongation de la terre, et avec le même télescope qui était excellent, la lune et ses taches n'étaient pas toujours également lumineuses, claires et visibles, mais qu'elles étaient plus brillantes, plus pures et plus distinctes dans un temps que dans un autre. Or, par les circonstances de cette observation, il est évident qu'il ne faut point chercher la raison de ce phénomène, ni dans notre air, ni dans la lune, ni dans l'oeil du spectateur, mais dans quelqu'autre chose qui environne le corps de la lune.
5°. Cassini a souvent observé que Saturne, Jupiter et les étoiles fixes, lorsqu'elles se cachaient derrière la lune, paraissaient près de son limbe, soit éclairé, soit obscur, changer leur figure circulaire en ovale ; et dans d'autres occultations, il n'a point trouvé du tout d'altération ; il arrive de même que le soleil et la lune se levant et se couchant dans un horizon vaporeux ne paraissent plus circulaires, mais elliptiques.
Or, comme nous savons par une expérience certaine que la figure circulaire du soleil et de la lune ne se changent en elliptique qu'à cause de la réfraction que les rayons de ces astres souffrent dans l'athmosphère, il est donc permis d'en conclure que dans les temps où la figure presque circulaire des étoiles est changée par la lune, cet astre est alors entouré d'une matière dense qui réfracte les rayons que les étoiles envaient ; et que si dans d'autres temps on n'observe point ce changement de figure, cette même matière ne se trouve plus autour de la lune. Voyez ATHMOSPHERE.
6°. La lune est donc un corps opaque, couvert de montagnes et de vallées. Riccioli a mesuré la hauteur d'une de ces montagnes, et a trouvé qu'elle avait neuf milles, ou environ 3 lieues de haut. Il y a de plus dans la lune de grands espaces, dont la surface est unie et égale, et qui réfléchissent en même temps moins de lumière que les autres. Or, comme la surface des corps fluides est naturellement unie, et que ces corps entant que transparents transmettent une grande partie de la lumière, et n'en réfléchissent que fort peu, plusieurs astronomes ont conclu de-là que les taches de la lune sont des corps fluides transparents, et que lorsqu'elles sont fort étendues, ce sont des mers. Il y a donc dans la lune des montagnes, des vallées et des mers. De plus, les parties lumineuses des taches doivent être par la même raison des îles et des péninsules. Et puisque dans les taches et près de leur limbe on remarque certaines parties plus hautes que d'autres, il faut donc qu'il y ait dans les mers de la lune des rochers et des promontoires.
Il faut avouer cependant que d'autres astronomes ont prétendu qu'il n'y avait point de mers dans la lune ; car si on regarde, disent-ils, avec un bon télescope les grandes taches que l'on prend pour des mers, on y remarque une infinité de cavernes ou de cavités très-profondes, ce qui s'aperçoit principalement par le moyen des ombres qui sont jetées au-dedans lorsque la lune croit, ou lorsqu'elle est en décours. Or c'est, ajoutent-ils, ce qui ne parait guère convenir à des mers d'une vaste étendue. Ainsi ils craient que ces régions de la lune ne sont point des mers, mais qu'elles sont d'une matière moins dure et moins blanche que les autres contrées des pays montueux.
7°. La lune est entourée, selon plusieurs astronomes, d'un athmosphère pesant et élastique, dans lequel les vapeurs et les exhalaisons s'élèvent pour retomber ensuite en forme de rosée ou de pluie.
Dans une éclipse totale du soleil, on voit la lune couronnée d'un anneau lumineux parallèle à sa circonférence.
Selon ces astronomes, on en a trop d'observations pour en douter. Dans la grande éclipse de 1715, on vit l'anneau à Londres, et par-tout ailleurs ; Kepler a observé qu'on a Ve la même chose à Naples et à Anvers dans une éclipse de 1605 ; et Wolf l'a observé aussi à Leipsick dans une de 1706, décrite fort au long dans les acta eruditorum, avec cette circonstance remarquable que la partie la plus voisine de la lune était visiblement plus brillante que celle qui en était plus éloignée, ce qui est confirmé par les observations des astronomes français dans les mémoires de l'Académie de l'année 1706.
Il faut donc, concluent-ils, qu'il y ait autour de la lune quelque fluide dont la figure corresponde à celle de cet astre, et qui tout-à-la-fais réfléchisse et brise les rayons du soleil ; il faut aussi que ce fluide soit plus dense près du corps de la lune, et plus rare au-dessus ; or comme l'air qui environne notre terre est un fluide de cette espèce, on peut conclure de-là que la lune doit avoir son air ; et puisque la différente densité de notre air dépend de sa différente gravité et élasticité, il faut donc aussi attribuer la différente densité de l'air lunaire à la même cause. Nous avons de plus observé que l'air lunaire n'est pas toujours également transparent, qu'il change quelquefois les figures sphériques des étoiles en ovales, et que dans quelques-unes des éclipses totales dont nous avons parlé, on a aperçu immédiatement avant l'immersion un tremblement dans le limbe de la lune avec une apparence d'une fumée claire et légère qui se tenait suspendue au-dessus durant l'immersion, et qui s'est fait fort remarquer en particulier en Angleterre ; et comme ces mêmes phénomènes s'observent aussi dans notre air quand il est plein de vapeur, il est donc presque sur que lorsqu'on les observe dans l'athmosphère de la lune, cette athmosphère doit être alors pleine de vapeurs et d'exhalaisons : enfin puisque dans d'autres temps l'air de la lune est clair et transparent, et qu'il ne produit aucun de ces phénomènes, il s'ensuit aussi que les vapeurs ont été alors précipitées sur la lune, et qu'il faut par conséquent qu'il soit tombé sur cet astre de la rosée, de la pluie ou de la neige.
Cependant d'autres astronomes prétendent que quand des étoiles s'approchent de la lune, elles ne paraissent souffrir aucune réfraction, ce qui prouverait que la lune n'a point d'athmosphère, du-moins telle que notre terre. Ils ajoutent qu'il y a beaucoup d'apparence que sur la lune il n'y a jamais de nuages, ni de pluies. Car s'il s'y trouvait des nuages, on les verrait, disent-ils, se répandre indifféremment sur toutes les régions du disque apparent, en sorte que ces mêmes régions nous seraient souvent cachées : or c'est ce qu'on n'a point observé. Il faut donc que le ciel de la lune soit parfaitement serein. Cependant les nuages pourraient se trouver dans la partie de l'athmosphère qui n'est point éclairée du soleil : car la chaleur qui est très-grande dans la partie éclairée, l'unique hémisphère qu'il nous est permis d'apercevoir, cette chaleur, dis-je, excitée par les rayons du soleil qui éclairent sans discontinuer ces régions de la lune pendant près de quinze fois 24 heures, suffit, ce semble, pour raréfier l'athmosphère de la lune. De plus, au sujet de cette athmosphère, M. le Monnier dit avoir remarqué en 1736 et 1738, que l'étoîle Aldebaran s'avançait en plein jour un peu sur le disque éclairé de la lune, où cette même étoîle disparut ensuite après avoir entamé très-sensiblement le disque, et cela vers le diamètre horizontal de la lune.
8°. La lune est donc à tous égards un corps semblable à la terre, et qui parait propre aux mêmes fins ; en effet, nous avons fait voir qu'elle est dense, opaque, qu'elle a des montagnes et des vallées ; selon plusieurs auteurs, elle a des mers avec des iles, des péninsules, des rochers et des promontoires, une athmosphère changeante où les vapeurs et les exhalaisons peuvent s'élever pour y retomber ensuite ; enfin elle a un jour et une nuit, un soleil pour éclairer l'un, et une lune pour éclairer l'autre, un été et un hiver, etc.
On peut encore conclure de-là par analogie une infinité d'autres propriétés dans la lune. Les changements auxquels son athmosphère est sujette, doivent produire des vents et d'autres météores, &, suivant les différentes saisons de l'année, des pluies, des brouillards, de la gelée, de la neige, etc. Les inégalités de la surface de la lune doivent produire de leur côté des lacs, des rivières, des sources, etc.
Or comme nous savons que la nature ne produit rien en vain, que les pluies et les rosées tombent sur notre terre pour faire végéter les plantes, et que les plantes prennent racine, croissent et produisent des semences pour nourrir des animaux ; comme nous savons d'ailleurs que la nature est uniforme et constante dans ses procédés, que les mêmes choses servent aux mêmes fins : pourquoi ne conclurions-nous donc pas qu'il y a des plantes et des animaux dans la lune ? A quoi bon sans cela cet appareil de provisions qui parait si bien leur être destiné ? Ces preuves recevront une nouvelle force, quand nous ferons voir que notre terre est elle-même une planète, et que si on la voyait des autres planètes, elle paraitrait dans l'une semblable à la lune, dans d'autres à Vénus, dans d'autres à Jupiter, etc. En effet, cette ressemblance, soit optique, soit physique, entre les différentes planètes, fournit une présomption bien forte qu'il s'y trouve les mêmes choses. Voyez TERRE et PLANETE.
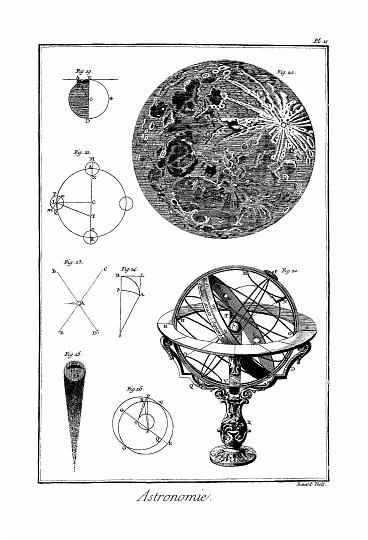
Moyen de mesurer la hauteur des montagnes de la lune. Sait E D, fig. 19. le diamètre de la lune, E C D le terme de la lumière et de l'ombre, et A le sommet d'une montagne situé dans la partie obscure, lequel commence à être éclairé ; observez avec un télescope le rapport que A E, c'est -à-dire la distance du point A à la ligne où la lumière commence, aura avec le diamètre E D, et vous aurez par-là deux côtés d'un triangle rectangle, savoir A E, C E, dont les carrés étant ajoutés ensemble, donneront le carré du 3e, voyez HYPOTHENUSE ; vous soustrairez de ce 3e côté le rayon C E, et il restera A B hauteur de la montagne. Riccioli a distingué les différentes parties de la lune par les noms des plus célèbres savants, et c'est par ces noms qu'on les marque toujours dans les observations des éclipses de lune, etc. Voyez en la figure, Pl. astron. fig. 20.
Parmi les autres observateurs qui ont tâché de représenter la figure de la lune, telle qu'on l'aperçoit avec des lunettes ordinaires, on compte principalement Langrenus, Hevelius et Grimaldi. Ils ont surtout représenté dans leur sénélographie, ou description de la lune, les plus belles taches. Hevelius qui appréhendait les guerres civiles qui se seraient élevées entre les Philosophes modernes, si on donnait leurs noms aux taches de la lune, au lieu de leur distribuer tout ce domaine, comme il se l'était proposé, jugea à propos d'y appliquer des noms de notre Géographie. Il est vrai que ces taches ne ressemblent guère, tant par rapport à leurs situations qu'à leurs figures, aux mers et aux continens de notre terre, dont ils portent le nom ; cependant on a recommandé jusqu'ici aux Astronomes, ces noms géographiques, qui ne sauraient leur devenir trop familiers, principalement à ceux qui veulent étudier dans Ptolémée la Géographie ancienne.
M. le Monnier prétend que toutes les figures de la lune qui ont été publiées jusqu'ici, celles qui ont été gravées en 1635 par le fameux D. Mellan, par ordre de Peiresc, sur les observations de Gassendi, et qui consiste en trois phases (dont l'une représente la pleine lune, et les deux autres le premier quartier et le décours), sont sans contredit les meilleures et les plus ressemblantes. Quoiqu'il n'y ait pas plus de vingt ans qu'elles sont devenues publiques, ces mêmes phases sont néanmoins les plus anciennes, puisqu'elles ont précédé celles d'Hevelius et de Riccioli, qui sont celles qu'on a le plus imitées, et dont les Astronomes ont le plus fait d'usage jusqu'à ce jour.
M. le Monnier a donné dans ses institutions astronomiques, pag. 140, trois différentes figures ou phases de la lune. La première est celle qu'Hevelius a publiée en 1645, avec les termes de la plus grande et de la plus petite libration ; la seconde a été publiée pour la première fois dans les mém. de l'académie royale des Sciences, pour l'année 1692 ; les termes de la plus grande et de la plus petite libration n'y sont point marqués, mais seulement la libration moyenne, c'est-à-dire les termes entre la plus grande et la plus petite. La troisième table que donne M. le Monnier est celle des PP. Grimaldi et Riccioli, avec la plus grande et la plus petite libration. Ces trois figures du disque de la lune sont assez différentes entr'elles.
On a attribué autrefois beaucoup de puissance à la lune sur les corps terrestres, et plusieurs personnes sont encore dans cette opinion, que les Philosophes regardent comme chimérique. Cependant si on examine la chose avec attention, il ne doit point paraitre impossible que la lune ne puisse avoir beaucoup d'influence sur l'air que nous respirons et les différents effets que nous observons. Il est certain que le soleil et la lune surtout, agissent sur l'Océan, et en causent le flux et le reflux. Or si l'action de ces astres est si sensible sur la masse des eaux, pourquoi ne le sera-t-elle pas sur l'athmosphère qui les couvre ? Pourquoi ne causera-t-elle pas dans cette athmosphère des mouvements et des altérations sensibles ? Il est vrai que le vulgaire tombe dans beaucoup d'erreurs à ce sujet, et nous ne prétendons point adopter tous les préjugés sur la nouvelle lune, sur les effets de la lune, tant en croissant ou en décours, sur les remèdes qu'il faut faire quand la lune est dans certains signes du zodiaque ; mais nous croyons pouvoir dire que plusieurs vents, par exemple, et les effets qui en résultent, peuvent être attribués très-vraisemblablement à l'action de la lune ; que par son action sur l'air que nous respirons, elle peut changer la disposition de nos corps, et occasionner des maladies : il est vrai que comme les dérangements qui arrivent dans l'athmosphère ont encore une infinité d'autres causes dont la loi ne parait point réglée, les effets particuliers de la lune se trouvant mêlés et combinés avec une infinité d'autres, sont par cette raison très-difficiles à connaître et à distinguer ; mais cela n'empêche pas qu'ils ne soient réels, et dignes de l'observation des Philosophes. Le docteur Mead, célèbre médecin anglais, a fait un livre qui a pour titre, de imperio solis ac lunae in corpore humano, de l'empire du soleil et de la lune sur les corps humains.
Jusqu'ici nous n'avons presque fait que traduire l'article lune tel qu'il se trouve à-peu-près dans l'encyclopédie anglaise, et nous y avons joint quelques remarques tirées de différents auteurs, entr'autres des institutions astronomiques de M. le Monnier. Il s'agit à présent d'entrer dans le détail de ce que les savants de notre siècle ont ajouté à la théorie de M. Newton.
Ce qu'on a lu jusqu'ici dans cet article contient les phénomènes du mouvement de la lune, tels à peu-près que les observations les ont fait connaître successivement aux Astronomes, et tels que M. Newton a tenté de les expliquer : nous disons a tenté, car quelque estimable que soit l'essai de théorie que ce grand homme nous a donné sur ce sujet, on a dû voir, par ce qui précède, que cet essai laisse encore beaucoup à désirer ; la raison en est que M. Newton n'avait point résolu le problème fondamental, nécessaire pour trouver les différentes irrégularités de la lune ; ce problème consiste à déterminer au moins par approximation, l'équation de l'orbite que la lune décrit autour de la terre ; c'est une branche du problème fameux connu sous le nom du problème des trois corps. Voyez PROBLEME DES TROIS CORPS.
La lune est attirée vers la terre en raison inverse du carré de la distance, suivant la loi générale de la gravitation (voyez GRAVITATION), et en même temps elle est attirée par le soleil ; mais comme la terre est aussi attirée par ce dernier astre, et qu'il s'agit ici non du mouvement absolu de la lune, mais de son mouvement par rapport à la terre, il faut transporter à la lune en sens contraire, l'action du soleil sur la terre, ainsi que la force avec laquelle la lune agit sur la terre (voyez les mém. de l'académie de 1745, pag. 365.) ; et en combinant ces différentes actions avec la force de gravitation de la lune vers la terre, il en résultera deux forces, l'une dirigée vers la terre, l'autre perpendiculaire au rayon vecteur. La force dirigée vers la terre est composée de deux parties, dont l'une est la force d'attraction de la lune vers la terre, et l'autre est très-petite par rapport à celle-là, et dépendante de celle du soleil. Il s'agit donc de trouver l'équation de la courbe, que la lune décrit en vertu de ces forces, et son intégration approchée ; or c'est ce que M. Euler, M. Clairaut et moi, avons trouvé en 1747 par différentes méthodes, qui toutes s'accordent quant au résultat. Je donnerai au mot PROBLEME DES TROIS CORPS, une idée de la mienne, qui me parait la plus simple de toutes ; mais quelque jugement qu'on en porte, il est certain que les trois méthodes conduisent exactement aux mêmes conclusions. La seule difficulté est dans la longueur peut-être du calcul. On peut en voir la preuve dans les ouvrages que Messieurs Euler, Clairaut et moi, avons publiés sur ce sujet. Celui de M. Euler a pour titre Theoria motus lunae ; celui de M. Clairaut est la pièce qui a remporté le prix à Petersbourg en 1751, et le mien est intitulé Recherches sur différents points importants du système du monde.
M. Euler est le premier qui ait imaginé de donner aux tables de la lune une nouvelle forme différente de celle de M. Newton ; au lieu de faire varier l'équation du centre, il regarde l'excentricité comme constante, et il ajoute à l'équation du centre une autre équation qu'on peut appeler évection (voyez EVECTION), et qui fait à peu-près le même effet que la variation supposée par M. Newton à l'excentricité, et au mouvement de l'apogée. M. Euler a publié le premier des tables suivant cette nouvelle forme, et dans lesquelles il a fait encore quelques autres changements à la forme des tables de M. Newton ; on peut voir sur cela le premier volume de ses opuscules, Berlin 1746 : mais ses tables très-commodes et très- expéditives pour le calcul, avaient le défaut de n'être pas assez exactes. M. Mayer, célèbre astronome de Gottingue, a perfectionné ces mêmes tables, en suivant la théorie de M. Euler, et en la corrigeant par les observations ; du reste il a conservé la forme donnée par M. Euler aux tables de la lune, et il l'a même encore simplifiée ; par ce moyen il a formé de nouvelles tables, qui ont paru en 1753, dans le second volume des mém, de l'acad. de Gottingue, et qui ont l'avantage d'être jusqu'ici les plus commodes et les plus exactes que l'on connaisse ; aussi l'académie royale des Sciences de Paris les a-t- elles adoptées par préférence à toutes les autres, dans la connaissance des temps pour l'année 1760 ; cependant malgré toutes les raisons qu'on a de croire les tables de M. Mayer plus exactes que les autres, il est nécessaire, pour n'avoir aucun doute là-dessus, de les comparer à un plus grand nombre d'observations ; et j'ai exposé dans la troisième partie de mes recherches sur le système du monde, les doutes qu'on pourrait encore former sur l'exactitude de ces mêmes tables, ou du-moins les raisons de suspendre son jugement à cet égard, jusqu'à ce qu'on en ait fait une plus longue épreuve.
M. Clairaut et moi avons aussi publié des tables de la lune suivant notre théorie ; celles de M. Clairaut, qui sont moins exactes que celles de M. Mayer, ont encore l'inconvénient de demander beaucoup plus de temps pour le calcul, parce qu'elles renferment un très-grand nombre d'équations. On assure que M. Clairaut a depuis ce temps perfectionné et simplifié beaucoup ces mêmes tables, mais il n'a encore rien publié de son travail dans le moment où nous écrivons ceci (le 15 Nov. 1759). Pour moi je me suis presque borné à donner d'après ma théorie, des tables de correction pour celle des institutions astronomiques ; mais j'ai reconnu depuis par la comparaison avec les observations et avec les meilleures tables, que ces tables de correction pourraient être perfectionnées à plusieurs égards ; non-seulement je les ai perfectionnées, mais j'ai plus fait, j'ai dressé des tables de la lune entièrement nouvelles, dont le calcul est très-expéditif, et qui, je crois, répondront assez exactement aux observations. Je n'en dirai pas davantage ici, parce que ces tables auront probablement Ve le jour avant que cet article paraisse.
Ces nouvelles tables sont dressées en partie sur les calculs que j'ai faits par théorie, en partie sur la comparaison que j'ai faite de mes premières tables avec celles de Messieurs le Monnier et Mayer, qui ont été comparées jusqu'ici à un plus grand nombre d'observations que les autres, et qui ont l'avantage de s'en écarter peu, et d'être d'ailleurs les plus expéditives pour le calcul, et les plus familières aux Astronomes. La raison qui m'a déterminé à ne pas dresser mes tables uniquement d'après la théorie, c'est l'épreuve que j'ai faite par mes propres calculs, et par ceux des autres, de la plupart des coefficiens des équations lunaires, dont on ne peut, ce me semble, assurer qu'aucun soit exact à une minute près, peut- être davantage. Cet inconvénient vient 1°. de ce que le nombre de petits termes et de petites quantités qui entrent dans chacun de ces coefficiens est si grand, qu'on n'est jamais assuré de n'en avoir point omis que puisse produire d'effet sensible. 2°. De ce que plusieurs des series qui expriment les coefficiens sont assez peu convergentes. 3°. Enfin de ce qu'il y a des termes qui étant très-petits dans la différencielle, peuvent devenir très-grands, ou au moins beaucoup plus grands par l'intégration. On peut voir les preuves de tout cela dans mes recherches sur le système du monde, première et troisième parties, et dans un écrit inséré à la fin de la seconde édition de mon traité de dynamique, en réponse à quelques objections qui m'avaient été faites sur ce sujet.
Une des preuves les plus frappantes de ce que j'avance ici sur l'incertitude des coefficiens des équations lunaires, c'est l'erreur où nous avons été longtemps Messieurs Euler, Clairaut et moi, sur le mouvement de l'apogée de la lune. Nous nous étions bornés tous trois à calculer d'abord le premier terme de la serie qui exprime ce mouvement, nous avons trouvé que ce terme ne donnait que la moitié du mouvement réel de l'apogée, parce que nous supposions tacitement que le reste de la serie pouvait se négliger par rapport au premier terme ; de-là M. Clairaut avait conclu que la gravitation n'était pas la raison inverse du carré des distances, mais qu'elle suivait quelqu'autre loi ; en quoi il faut avouer que sa conclusion a été trop précipitée, puisque quand même le mouvement de l'apogée trouvé par la théorie ne serait que la moitié de ce qu'il est réellement, on pourrait sans changer la loi d'attraction et y substituer une loi bizarre, attribuer cet effet comme je l'avais imaginé, à quelque cause particulière différente de la gravitation, comme à la force magnétique, dont M. Newton fait mention expressément. On peut voir dans les mém. de l'acad. des Sciences de 1745, la dispute de Messieurs Clairaut et de Buffon sur ce sujet. On peut aussi consulter l'article ATTRACTION, et mes recherches sur le système du monde, première partie, art. 173. Quoi qu'il en sait, M. Clairaut s'aperçut le premier de l'erreur commune à nos calculs, et me communiqua la remarque qu'il en avait faite ; on peut en voir le détail dans mes recherches sur le système du monde, art. 107 et suivants. Il m'apprit qu'ayant voulu calculer le second terme de la serie du mouvement de l'apogée, pour connaître à très-peu près ce que le fond de la gravitation donnait pour le mouvement, il lui était venu un second terme qui n'était pas fort différent du premier, ce qui rendait à la gravitation tout son effet pour produire le mouvement entier de l'apogée. Cette remarque, il faut l'avouer, était très-forte en faveur de la gravitation ; cependant il est évident qu'elle ne suffit pas encore pour décider la question ; car puisque les deux premiers termes de la serie étaient presqu'égaux, le troisième pouvait l'être encore aux deux premiers ; et en ce cas, selon le signe de ce troisième terme, on aurait trouvé le mouvement de l'apogée beaucoup plus grand ou beaucoup plus court qu'il ne fallait pour la théorie de la gravitation. Il était donc absolument nécessaire de calculer ce troisième terme, et même quelques-uns des suivants, pour s'assurer si la théorie de la gravitation répondait en effet aux phénomènes ; car jusques-là, je le répete, il n'y avait encore rien de décidé. J'entrepris donc ce calcul, que jusqu'ici aucun autre géomètre n'a fait encore. J'en ai donné le résultat dans mes recherches sur le système du monde, au chap. xx. de la première partie, et il en résulte que le mouvement de l'apogée trouvé par la théorie, est tel que les observations le donnent. Voilà ce que l'Astronomie doit à M. Clairaut et à moi sur cette importante matière.
Une autre remarque qui m'est entièrement dû., et que je communiquai à M. Clairaut au mois de Juin 1748, c'est le calcul des termes, qui dans l'équation de l'orbite lunaire ont pour argument la distance du soleil à l'apogée de la lune. M. Clairaut croyait alors, faute d'avoir calculé tous les termes essentiels qui entrent dans cette équation, qu'elle montait à environ 35 ou 40 minutes ; ce qui, comme M. Clairaut le croyait alors, renversait entièrement la théorie et le système newtonien ; je lui fis voir que cette équation était beaucoup moindre, et de deux à trois minutes seulement ; ce qui rétablissait la théorie dans tous ses droits.
Je ne dois pas oublier d'ajouter 1°. que ma méthode pour déterminer le mouvement de l'apogée, est très-élégante et très-simple, n'ayant besoin d'aucune intégration, et ne demandant que la simple inspection des coefficiens du second terme de l'équation différencielle ; 2°. que j'ai démontré le premier par une méthode rigoureuse, ce que personne n'avait encore fait, et n'a même fait jusqu'ici, que l'équation de l'orbite lunaire ne devait point contenir d'arcs de cercle ; si on ajoute à cela la manière simple et facîle dont je parviens à l'équation différentielle de l'orbite lunaire, sans avoir besoin pour cela, comme d'autres géomètres, de transformations et d'intégrations multipliées ; et le détail que j'ai donné ci-dessus de mes travaux et de ceux des autres géomètres, on conviendra, ce me semble, que j'ai eu plus de part à la théorie de la lune que certains mathématiciens n'avaient voulu le faire croire. Je ne dois pas non plus passer sous silence la manière élégante dont M. Euler intègre l'équation de l'orbite lunaire ; méthode plus simple et plus facîle que celle de M. Clairaut et que la mienne ; et cette observation jointe à ce que j'ai dit plus haut des travaux de ce grand géomètre, par rapport à la lune, suffira pour faire voir qu'il a aussi travaillé très-utilement à cette théorie, quoiqu'on ait aussi cherché à le mettre à l'écart autant qu'on l'a pu. L'Encyclopédie faite pour transmettre à la postérité l'histoire des découvertes de notre siècle, doit par cette raison rendre justice à tout le monde ; et c'est ce que nous croyons avoir fait dans cet article. Comme ce manuscrit est prêt à sortir de nos mains pour n'y rentrer peut être jamais, nous ajouterons par la suite dans les suppléments de l'Encyclopédie ce qui aura été ajouté à la théorie de la lune, depuis le mois de Novembre 1759, où nous écrivons cet article.
Nous avons dit plus haut que M. Halley avait commencé l'observation d'une période de deux cent vingt-trois lunaisons, et que M. le Monnier avait continué ce travail ; le public en a déjà recueilli le fruit, M. le Monnier ayant publié deux volumes de ses observations, qui serviront à connaître l'erreur des tables ; il continue ce travail avec ardeur et avec assiduité ; et il espère publier successivement le résultat de ses observations à la fin de chaque période ; au reste il ne faut pas croire, comme je l'ai remarqué et prouvé ce me semble le premier dans mes recherches sur le système du monde, troisième partie, qu'au bout de la période de deux cent vingt-trois lunaisons, les inégalités reviennent exactement les mêmes, mais la différence n'est pas bien considérable, et au moyen d'une méthode facîle que j'ai indiquée, on peut déterminer assez exactement l'erreur des tables pour chaque lieu calculé de la lune. Voyez l'article xxxj. de l'ouvrage cité.
Pour achever de rendre compte des travaux des Géomètres de notre siècle sur la lune, il ne nous reste plus qu'à parler de leurs recherches sur la masse de cette planète. M. Newton, par quelques phénomènes des marées, avait essayé de la déterminer. Voyez FLUX et REFLUX. M. Daniel Bernoulli a depuis corrigé ce calcul ; enfin par une théorie de la précession des équinoxes et de la nutation, j'ai déterminé la masse de la lune d'environ un 1/75 de celle de la terre ; c'est-à-dire environ la moitié de ce qu'avait trouvé M. Newton ; ce calcul est fondé sur ce que la nutation de l'axe de la terre vient presqu'uniquement de la force lunaire, et qu'au contraire la précession vient de la force lunaire et de la force solaire réunies ; d'où il s'ensuit qu'on trouvera le rapport des deux forces, en comparant la quantité observée de la nutation avec la quantité observée de la précession. Or le rapport des forces étant connu, on en déduit aisément la masse de la lune. Voyez mes recherches sur la précession des équinoxes, 1749, et la seconde partie de mes recherches sur le système du monde, liv. III. art. IIIe voyez aussi les articles NUTATION et PRECESSION.
J'ajouterai ici que dans l'hypothèse de la non-sphéricité de la lune, la terre et le soleil doivent produire dans l'axe de cette planète un mouvement analogue à celui que l'action de la lune et du soleil produisent dans l'axe de la terre, et d'où résulte la précession des équinoxes ; sur quoi voyez mes recherches sur le système du monde seconde partie, articles cccxliij. et suiv. voyez aussi l'article LIBRATION. Au reste, si les diamètres de la lune sont inégaux, leur inégalité est très-peu sensible par les observations, comme je l'ai prouvé dans les mêmes recherches, seconde partie, art. ccclxxvj. et suiv. (O)