Aristote et ses sectateurs divisent le lieu en interne et en externe.
Le lieu interne est cet espace ou cette place qu'un corps contient.
Le lieu externe est celui qui renferme le corps : Aristote l'appelle encore la première surface concave et immobîle du corps environnant.
On dispute fort dans les écoles sur la question du lieu interne. On demande, si c'est un être réel qui existe indépendamment des corps, ou seulement un être imaginaire ; c'est-à-dire, si c'est seulement une aptitude et une capacité de recevoir des corps ?
Il y en a qui soutiennent que c'est un être positif, incorporel, éternel, indépendant et infini ; et ils poussent leur assertion jusqu'à prétendre que le lieu interne constitue l'immensité de Dieu.
Les Cartésiens, au contraire, soutiennent que le lieu interne, considéré par abstraction, n'est pas différent de l'étendue des corps qui y sont contenus, et qu'ainsi il ne diffère en rien des corps eux-mêmes. Voyez MATIERE.
Les Scholastiques mettent pareillement en question, si le lieu externe est mobîle ou immobile. On déduit son immobilité de cette considération, que tout ce qui se meut doit nécessairement quitter sa place ; ce qui ne pourrait arriver, si le lieu s'en allait avec le mobîle ; car si le lieu se mouvait avec le mobile, le mobîle ne changerait pas de place. D'autres traitent d'absurde cette opinion d'Aristote ; ils prétendent que si un corps en mouvement change de lieu en ce sens qu'il répond continuellement par la surface extérieure à différents corps ou à différentes parties de l'espace, on devrait dire par la même raison qu'un corps réellement en repos change continuellement de place.
Par exemple, qu'une tour dans une plaine, ou un rocher au milieu de la mer, sont continuellement en mouvement, ou changent de place, à cause que l'un et l'autre sont perpétuellement enveloppés de nouvel air ou de nouvelle eau.
Pour résoudre cette difficulté, on a eu recours à une infinité d'expédiens. Les Scotistes tiennent que le lieu n'est immobîle qu'équivalemment. Ainsi, disent-ils, quand le vent souffle, il est vrai que l'air qui environne la surface de la tour s'en éloigne ; mais tout de suite un autre air semblable et équivalent en prend la place. Les Thomistes aiment mieux déduire l'immobilité du lieu externe, de ce qu'il garde toujours la même distance au centre et aux points cardinaux du monde. Les Nominaux prétendent que l'immobilité du lieu externe consiste dans une correspondance avec certaine partie virtuelle de l'immensité divine. Nous passons légèrement sur toutes ces rêveries qui doivent nécessairement trouver leur place dans un ouvrage destiné à l'histoire de l'esprit humain, mais qui ne doivent aussi y occuper que très-peu d'espace.
Les Cartésiens nient absolument que le lieu externe soit une surface environnante ou un corps environné : ils prétendent que c'est seulement la situation d'un corps parmi d'autres corps voisins, considéré comme en repos. Ainsi la tour, disent-ils, sera réputée rester dans le même lieu, quoique l'air environnant soit changé, puisqu'elle conserve toujours la même situation par rapport aux montagnes, aux arbres et aux autres parties de la terre qui sont en repos. Voyez MOUVEMENT.
Il est visible que la question du lieu tient à celle de l'espace. Voyez ESPACE et ÉTENDUE.
Les Cartésiens ont raison, si l'espace et l'étendue ne sont rien de réel et de distingué de la matière ; mais si l'étendue ou l'espace et la matière sont deux choses différentes, il faut alors regarder le lieu comme une chose distinguée des corps, et comme une partie immobîle et pénétrable de l'espace indéfini : on peut voir aux articles cités la discussion de cette opinion ; il est certain que suivant notre manière ordinaire de concevoir, et indépendamment de toute subtilité philosophique, il y a un espace indéfini que nous regardons comme le lieu général de tous les corps, et que les différentes parties de cet espace, lesquelles sont immobiles, sont le lieu particulier des différents corps qui y répondent. Au reste, comme on l'a remarqué au mot ÉLEMENS DES SCIENCES, cette question du lieu est absolument inutîle à la théorie du mouvement tel que tous les hommes le conçoivent. Quoi qu'il en sait, c'est de cette idée vulgaire et simple de l'espace et du lieu qu'on doit partir quand on voudra donner une notion simple et claire du mouvement.
C'est aussi d'après cette idée que M. Newton distingue le lieu en lieu absolu et en lieu relatif.
Le lieu absolu est cette partie de l'espace infini et immobîle qui est occupée par un corps.
Le lieu relatif est l'espace qu'occupe un corps considéré par rapport aux autres objets qui l'environnent.
M. Locke observe que le lieu se prend aussi pour cette portion de l'espace infini que le monde matériel occupe ; il ajoute cependant que cet espace serait plus proprement appelé étendue.
La véritable idée du lieu, selon lui, est la position relative d'une chose par rapport à sa distance de certains points fixes ; ainsi nous disons qu'une chose a ou n'a pas changé de place ou de lieu, quand sa distance n'a point changé par rapport à ces points. Quant à la vision du lieu des corps. Voyez VISION et VISIBLE.
Lieu dans l'optique ou lieu optique, c'est le point auquel l'oeil rapporte un objet.
Ainsi les points D, E, (Pl. opt. fig. 68.) auxquels deux spectateurs en d et en e rapportent l'objet C, sont appelés lieux optiques. Voyez VISION.
Si une ligne droite joignant les lieux optiques D, E, est parallèle à une ligne droite qui passe par les yeux des spectateurs d, e, la distance des lieux optiques D, E sera à la distance des spectateurs d, e, comme la distance E C est à la distance C e.
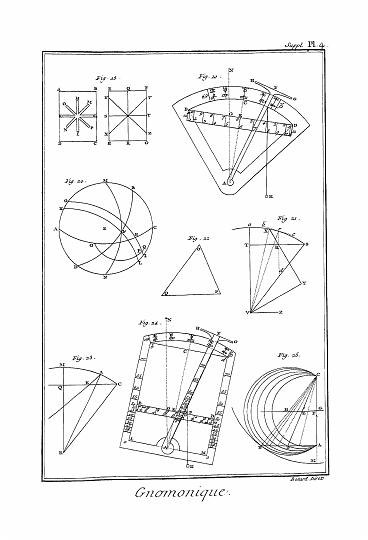
Le lieu optique ou simplement le lieu d'une étoîle ou d'une planète, est un point dans la surface de la sphère du monde, comme C ou B (Pl. ast. fig. 27.) auquel un spectateur placé en E ou en I, rapporte le centre de l'étoîle ou de la planète S. Voyez ÉTOILE, PLANETE, etc.
Ce lieu se divise en vrai et en apparent. Le lieu vrai est ce point B de la surface de la sphère où un spectateur, placé au centre de la terre, voit le centre de l'étoîle ; ce point se détermine par une ligne droite, tirée du centre de la terre par le centre de l'étoile, et terminée à la sphère du monde. Voyez SPHERE.
Le lieu apparent, est ce point de la surface de la sphère, où un spectateur placé sur la surface de la terre en E, voit le centre de l'étoîle S. Ce point C se trouve par le moyen d'une ligne qui Ve de l'oeil du spectateur à l'étoile, et se termine dans la sphère des étoiles. Voyez APPARENT.
La distance entre ces deux lieux optiques, savoir le vrai et l'apparent, fait ce qu'on appelle la parallaxe. Voyez PARALLAXE.
Le lieu astronomique du soleil, d'une étoîle ou d'une planète, signifie simplement le signe et degré du zodiaque, où se trouve un de ces astres. Voyez SOLEIL, ÉTOILES, etc.
Ou bien c'est le degré de l'écliptique, à compter du commencement d'Aries, qui est rencontré par le cercle de longitude de la planète ou de l'étoile, et qui par conséquent indique la longitude du soleil, de la planète ou de l'étoile. Voyez LONGITUDE.
Le sinus de la plus grande déclinaison du soleil, qui est environ 23°. 30'. est au sinus d'une déclinaison quelconque actuelle, donné ou observé, par exemple, 23°. 15', comme le rayon est au sinus de la longitude ; ce qui donnerait, si la déclinaison était septentrionale, le 20°. 52'. des gémeaux ; et si elle était méridionale, 20°. 52'. du capricorne pour le lieu du soleil.
Le lieu de la lune est le point de son orbite où elle se trouve en un temps quelconque. Voyez LUNE et ORBITE.
Le lieu est assez long à calculer à cause des grandes inégalités qui se rencontrent dans les mouvements de la lune, ce qui exige un grand nombre d'équations et de réductions avant que l'on trouve le lieu vrai. Voyez ÉQUATION et LUNE.
Le lieu excentrique d'une planète dans son orbite, est le lieu de l'orbite où paraitrait cette planète, si on la voyait du soleil. Voyez EXCENTRIQUE.
Ainsi supposons que N E O R (Pl. ast. fig. 26.) soit le plan de l'écliptique, N P O Q, l'orbite de la planète, le soleil en S, la terre en T, et la planète en P ; la ligne droite S P donne le lieu excentrique dans l'orbite.
Le lieu héliocentrique d'une planète ou son lieu réduit à l'écliptique, ou bien le lieu excentrique dans l'écliptique, est ce point de l'écliptique, auquel on rapporte une planète vue du soleil. Voyez HELIOCENTRIQUE.
Si on tire la perpendiculaire P S à l'écliptique, la ligne droite R S, indique le lieu héliocentrique ou le lieu réduit à l'écliptique.
Le lieu géocentrique est ce point de l'écliptique, auquel on rapporte une planète vue de la terre. Voyez GEOCENTRIQUE.
Ainsi NEOR représentant l'écliptique, etc. T, R donnera le lieu géocentrique. Sur le calcul du lieu d'une planète, voyez PLANETE, ÉQUATION, etc. Chambers. (O)
LIEU GEOMETRIQUE, signifie une ligne par laquelle se résout un problème géométrique. Voyez PROBLEME et GEOMETRIQUE.
Un lieu est une ligne dont chaque point peut également résoudre un problème indéterminé. S'il ne faut qu'une droite pour construire l'équation du problème, le lieu s'appelle alors lieu à la ligne droite ; s'il ne faut qu'un cercle, lieu au cercle ; s'il ne faut qu'une parabole, lieu à la parabole ; s'il ne faut qu'une ellipse, lieu à l'ellipse ; et ainsi des autres, etc.
Les anciens nommaient lieux plans, les lieux des équations qui se réduisent à des droites ou à des cercles ; et lieux solides ceux qui sont ou des paraboles, ou des hyperboles, ou des ellipses.
M. Wolf donne une autre définition des lieux, et il les range en différents ordres, selon le nombre de dimensions auxquelles la quantité indéterminée s'élève dans l'équation. Ainsi ce sera un lieu du premier ordre, si l'équation est x =
Pour mieux concevoir la nature des lieux géométriques, supposons deux droites inconnues et variables A P, P M (Pl. d'analyse, fig. 29, 30), qui fassent entr'elles un angle donné quelconque. A P M, dont nous nommerons l'une, par exemple A P, qui a son origine fixe en A, et qui s'étend indéfiniment dans une direction donnée, Xe et l'autre P M, qui change continuellement de position et de grandeur, mais qui reste toujours parallèle à elle-même, y. Supposons de plus une équation qui ne contienne d'inconnues que ces deux quantités Xe y, mêlées avec des quantités connues, et qui exprime le rapport de la variable A P, Xe à la valeur de P M, ou de l'y correspondante ; enfin imaginons qu'à l'extrémité de chaque valeur possible de Xe on ait tracé en effet l'y correspondante que cette équation détermine ; la ligne droite ou courbe qui passera par les extrémités de toutes les y ainsi tracées, ou par tous les points M, sera nommée en général lieu géométrique, et lieu de l'équation proposée en particulier.
Toutes les équations dont les lieux sont du premier ordre peuvent se réduire à quelqu'une des quatre formules suivantes : 1°. y = : 2°. y = + c : 3°. y = - c : 4°. y = c - , dans lesquelles la quantité inconnue y est supposée toujours avoir été délivrée de fractions, la fraction qui multiplie l'autre inconnue x est supposée réduite à cette expression b/a ; et tous les autres termes sont comme censés réduits à celui + c. Le lieu de la première formule est d'abord déterminé, puisqu'il est évident que c'est une droite qui coupe l'axe dans son origine A, et qui fait avec lui un angle tel que les deux inconnues Xe y soient toujours entr'elles comme a est à b. Or supposant ce premier lieu connu, il faudra pour trouver celui de la seconde formule y = + c, prendre d'abord sur la ligne A P (fig. 31.), une partie A B = a, et tirer B E = b et A D = c parallèles à P M. Vous tirerez ensuite du même côté que A P et vers E la ligne A E d'une longueur indéfinie, et la ligne droite et indéfinie D M parallèle à A E ; je dis que la ligne D M est le lieu de l'équation, ou la formule que nous voulions construire. Car si par un point quelconque M de cette ligne, on tire M P parallèle à A Q, les triangles A B E, A P F, seront semblables ; ce qui donnera A B, a, B E, b : : A P, Xe P F = , et par conséquent P M (y) = P F () + F M (c). Si on fait c = 0, c'est-à-dire si les points D A tombent l'un sur l'autre, et D M sur A F, la ligne A F sera alors le lieu de l'équation y = . Pour trouver le lieu de la troisième formule, il faudra s'y prendre de cette sorte : vous ferez A B = a (fig. 32.) et vous tirerez les droites B E = b, A D = c parallèles à P M, l'une de l'un des côtés de A P, et l'autre de l'autre côté : par les points A, E, vous tirerez la droite A E, que vous prolongerez indéfiniment vers E, et par le point D la ligne D M, parallèle à A E, je dis que la droite indéfinie G M sera le lieu cherché. Car nous aurons toujours P M (y) = P F, () - F M (c). Enfin pour trouver le lieu de la quatrième formule, sur A P (fig. 33.), vous prendrez A B = a, et vous tirerez B E = b, et A D = c, l'une d'un des côtés de A P, et l'autre de l'autre côté. De plus, par les points A, E, vous tirerez A E, que vous prolongerez indéfiniment vers E, et par le point D la ligne D M parallèle à A E, je dis que D G sera le lieu cherché. Car si par un de ses points quelconques M on tire la ligne M P parallèle à A Q, on aura toujours P M (y) = F M (c) - P F ().
Il s'ensuit de là qu'il n'y a de lieu du premier degré que les seules lignes droites ; ce qui peut se voir facilement, puisque toutes les équations possibles du premier degré se réduisent à l'une des formules précédentes.
Tous les lieux du second degré ne peuvent être que des sections coniques, savoir la parabole, l'ellipse ou le cercle, qui est une espèce d'ellipse, et l'hyperbole, qui dans certains cas devient équilatère : si on suppose donc donnée une équation indéterminée, dont le lieu soit du second degré, et qu'on demande de décrire la section conique qui en est le lieu ; il faudra commencer par considérer une parabole, une ellipse et une hyperbole quelconque, en la rapportant à des droites ou des coordonnées, telles que l'équation qui en exprimera la nature, se trouve être par là la plus composée et la plus générale qu'il soit possible. Ces équations les plus générales, ou ces formules de trois sections coniques et de leurs subdivisions étant découvertes, et en ayant examiné les caractères, il sera aisé de conclure à laquelle d'entr'elles se rapportera l'équation proposée, c'est-à-dire quelle section conique cette même équation aura pour lieu. Il ne s'agira plus après cela que de comparer tous les termes de l'équation proposée avec ceux de l'équation générale du lieu, auquel on aura trouvé que cette équation se rapporte, cela déterminera les coefficiens de cette équation générale, ou ce qui est la même chose, les droites qui doivent être données de proportion et de grandeur pour décrire le lieu ; et ces coefficiens, ou ces droites étant une fois déterminées, on décrira facilement le lieu, par les moyens que les traités des sections coniques fournissent.
Par exemple que A P, Xe P M, y soient deux droites inconnues et variables (fig. 34) ; et que m, p, r, s, soient des droites données ; sur la ligne A P, prenez la portion A B = m, et tirez B E = n, A D = r ; et par le point A, tirez A E = e, et par le point D, la ligne indéfinie D G parallèle à A E ; sur D G, prenez D C = s, et prenant C G pour diamètre, les ordonnées parallèles à P M, et la ligne C H = p pour paramètre, décrivez la parabole C M, et elle sera le lieu de la formule générale suivante.
y y - x y + x x = 0.
- 2 r y + . x
- x
+ r r
+ p s.
car si d'un de ses points quelconques M on tire l'ordonnée P M, les triangles A B E, A P F, seront semblables, et par conséquent
A B (m) : A E (e) : : A P (x) : A F ou D G =
Cette équation est la plus générale qui puisse appartenir à la parabole, puisqu'elle renferme 1°. le carré de chacune des inconnues Xe y ; 2°. le produit x y de l'une par l'autre ; 3°. les inconnues linéaires Xe y, et un terme tout constant. Une équation du second degré, ou les indéterminées Xe y, se trouvent mêlées, ne saurait contenir un plus grand nombre de termes.
Par le point fixe A, tirez la droite indéfinie A Q, (fig. 35.) parallèle à P M ; prenez A B = m, tirez B E = n parallèle à A P, et par les points déterminés A E, la droite A E = e ; sur A P, prenez A D = r, tirez la droite indéfinie D G, parallèle à A E, et prenez la portion D C = s. Enfin prenant pour diamètre C G, et supposant les ordonnées parallèles à A P, et pour paramètre la ligne C H = p, décrivez une parabole C M ; cette parabole serait le lieu de cette seconde équation ou formule.
x x - y x + y y = o.
- 2 r x - y
+ r r
+ p s.
car si d'un point quelconque M on tire la droite M Q parallèle à A P, on aura A B (m) : A E (e) : : A Q ou P M (y) : A F ou D G = et A B (m) : B E (n) : : A Q (y) : Q F = , et par conséquent G M ou Q M - Q F - F G = x - - r ; et C G ou D G - D C = - s : et ainsi par la propriété de la parabole, vous trouverez encore la seconde des équations générales ou des formules précédentes ; et vous vous y prendrez de la même sorte, pour trouver les équations générales ou les formules des autres sections coniques.
Si on demande maintenant de décrire la parabole qui doit être le lieu de l'équation suivante, que nous supposerons donnée y y - 2 a y - b x + c c = 0, comme y y se trouve ici sans fraction, de même que dans notre première formule, il vaudra mieux comparer la proposée avec cette première formule qu'avec l'autre ; et d'abord puisque le rectangle x y ne se trouve point dans la proposée, ou qu'il peut y être censé multiplié par 0, nous en conclurons que la fraction
Or les valeurs de m, n, r, p, s, ayant été ainsi trouvées, on construira facilement le lieu cherché par les moyens qui nous ont servi à la construction de la formule et de la manière suivante, comme B E (n) est = 0 (fig. 36.) et que les points B, E, coincident, ou que A E tombe sur A P, il faudra par cette raison tirer du point A la droite A D (r) parallèle à P M et = a, et la droite D G parallèle à A P, dans laquelle vous marquerez la droite D C (s) =
Voilà une idée de la méthode de construire les lieux des équations lorsqu'ils doivent être des sections coniques, ou ce qui est la même chose, lorsque les équations ne passent pas le second degré : car on doit sentir que les lieux à l'ellipse et à l'hyperbole, doivent se déterminer par une méthode semblable.
Mais une pareille équation étant donnée, au lieu de demander comme tout-à-l'heure, d'en construire le lieu, si on se contente de demander quelle doit être l'espèce de la section conique qui en est le lieu, si c'est une parabole, une ellipse ou même un cercle, un hyperbole équilatère, ou non équilatère, il faudrait pour en juger, commencer par faire passer d'un même côté tous les termes de l'équation, de façon qu'il restât zero de l'autre côté ; et cela étant fait, il pourrait se présenter deux cas différents.
Premier cas ; supposons que le rectangle x y, ne se trouve point dans l'équation ; alors 1°. s'il n'y a qu'un des deux carrés y y, ou x Xe le lieu sera une parabole. 2°. Si les deux carrés s'y trouvent tout-à-la-fais et avec le même signe, le lieu sera une ellipse, et en particulier un cercle, lorsque ni l'un ni l'autre des deux carrés n'aura de coefficient, ou (si on n'avait point réduit l'un d'eux à n'en point avoir), lorsqu'ils auront les mêmes coefficiens, et que de plus l'angle des coordonnées sera droit. 3°. si les deux carrés x Xe et y y se trouvent dans l'équation, et avec des signes différents, le lieu sera une hyperbole laquelle deviendra équilatère dans les mêmes suppositions, qui font de l'ellipse un cercle.
Second cas ; quand le rectangle x y se trouve dans l'équation, alors 1°. s'il ne s'y trouve aucun des deux carrés, qu'il ne s'y en trouve qu'un, ou encore qu'ils s'y trouvent tous deux avec différents signes, ou enfin que s'y trouvant tous deux avec les mêmes signes, le carré du coefficient qui multiplie x y, soit plus grand que le quadruple du rectangle des coefficiens de x x et y y, dans toutes ces suppositions le lieu sera une hyperbole. 2°. Si ces deux carrés s'y trouvant toujours, et étant de même signe ; si le carré du coefficient x y, est plus petit que le quadruple du rectangle des coefficiens de x x et y y, le lieu sera alors une ellipse. 3°. Enfin, si dans la même supposition ce carré et le quadruple du rectangle dont nous venons de parler, sont égaux entr'eux, le lieu sera alors une parabole.
Cette méthode de construire les lieux géometriques, en les rapportant aux équations les plus composées qu'il soit possible, est dû. à M. Craig, auteur anglais, qui l'a publiée le premier dans son traité de la quadrature des courbes, en 1693. Elle est expliquée fort au long dans le septième et le huitième livre des sections coniques de M. le Marquis de l'Hôpital, qui sans doute en aurait fait honneur au géomètre anglais, s'il eut eu le temps de mettre la dernière main à son ouvrage.
M. Guisnée, dans son application de l'Algèbre à la Géométrie, donne une autre méthode pour construire les lieux géométriques. Elle est plus commode à certains égards que la précédente, en ce qu'elle apprend à construire tout d'un coup et immédiatement une équation donnée, sans la rapporter à une équation plus générale ; mais d'un autre côté elle demande aussi dans la pratique plus de précaution pour ne se point tromper.
Nous ne devons pas oublier de dire que M. l'abbé de Gua, dans les usages de l'analyse de Descartes, pag. 342, remarque une espèce de faute qu'on pourrait reprocher aux auteurs qui ont écrit jusqu'ici sur la construction des lieux géométriques, et fait voir cependant que cette faute n'a point dû tirer à conséquence dans les règles ou les méthodes que ces auteurs ont données.
Cette faute, qu'il serait trop long de détailler ici, consiste en général en ce que ces auteurs n'ont enseigné à réduire à l'hyperbole entre ses asymptotes, que les lieux où il manque un des carrés Xe y. On peut réduire à l'hyperbole entre ses asymptotes une équation même qui contiendrait ces deux carrés, mais alors aucune des deux asymptotes ne serait parallèle à la ligne des Xe ni à celle des y. Voyez TRANSFORMATION DES AXES ; voyez aussi sur les lieux en général, et sur ceux aux sections coniques en particulier ; les articles COURBE, EQUATION, CONIQUE, ELLIPSE, CONSTRUCTION, etc. (O)
LIEUX-COMMUNS, (Rhétorique) ce sont dans l'art oratoire, des recueils de pensées, de réflexions, de sentences, dont on a rempli sa mémoire, et qu'on applique à propos aux sujets qu'on traite, pour les embellir ou leur donner de la force. Démosthène n'en condamne pas l'emploi judicieux ; il conseille même aux orateurs qui doivent souvent monter sur la tribune pour y traiter différents sujets, de faire une provision d'exordes et de péroraisons. Cicéron, (& nous n'avons rien au dessus de ses préceptes, ni peut-être de ses exemples) voulait, de plus que Démosthène, qu'on eut des sujets entiers traités d'avance et des discours préparés dans l'occasion, aux noms et aux circonstances près ; mais ces beaux génies n'avaient-ils pas un fond assez riche dans leur propre enthousiasme, et dans la fécondité de leurs talents, sans recourir à ces sortes de ressources ? Il semble que leur méthode ne pouvait guère être d'usage que pour les esprits médiocres qui faisaient à Athènes et à Rome une espèce de trafic de l'éloquence. Cette même méthode servirait encore moins dans notre barreau, où l'on ne traite que de petits objets de droit écrit et de droit coutumier, dans lesquels il ne s'agit que d'exposer ses demandes ou ses moyens d'appel, selon les règles de la jurisprudence des lieux. (D.J.)
LIEUX, les, s. m. pl. (Architecture moderne) terme synonyme à aisance, commodités, privés. Voyez ces trois mots.
On pratique ordinairement les lieux à rez-de-chaussée, au haut d'un escalier ou dans les angles. Dans les grands hôtels et dans les maisons commodes, on les place dans de petits escaliers, jamais dans les grands ; dans les maisons religieuses et de communauté, les aisances sont partagées entre plusieurs cabinets de suite, avec une cuillier de pierre, percée pour la décharge des urines.
Elles doivent être carrelées, pavées de pierre ou revêtues de plomb, et en pente du côté du siege, avec un petit ruisseau pour l'écoulement des eaux dans la chaussée, percée au bas de la devanture.
On place présentement les aisances dans les garderobes, où elles tiennent lieux de chaises percées : on les fait de la dernière propreté, et en forme de baguette, dont le lambris se lève et cache la lunette. La chaussée d'aisance est fort large et fort profonde, pour empêcher la mauvaise odeur : on y pratique aussi de larges ventouses ; le boisseau qui tient à la lunette est en forme d'entonnoir renversé, et soutenu par un cercle de cuivre à feuillure, dans lequel s'ajuste une soupape de cuivre, qui s'ouvre et se ferme en levant et fermant le lambris du dessus, ce qui empêche la communication de la mauvaise odeur. On pratique dans quelque coin de ces lieux, ou dans les entresolles au-dessus, un petit réservoir d'eau, d'où l'on amène une conduite, à l'extrémité de laquelle est un robinet qui sert à laver les urines qui pourraient s'être attachées au boisseau et à la soupape. On pratique aussi une autre conduite qui vient s'ajuster dans le boisseau, et à l'extrémité de laquelle est un robinet. Ce robinet se tire au moyen d'un registre vers le milieu du boisseau, ce qui sert à se laver à l'eau chaude et à l'eau froide, suivant les saisons. Ces robinets s'appellent flageolets, et ces aisances lieux à l'anglaise, parce que c'est aux Anglais qu'on en doit l'invention. (D.J.)
LIEU, (Maréchalerie) ce terme se dit de la posture et de la situation de la tête du cheval ; ainsi un cheval qui porte en beau lieu, ou simplement qui porte beau, est celui qui soutient bien son encolure, qui l'a élevée, et tournée en arc comme le cou d'un cygne, et qui tient la tête haute sans contrainte, ferme et bien placée. Voyez ENCOLURE.
LIEU HILEGIAUX, en terme d'Astrologie, sont ceux qui donnent à la planète qui s'y trouve le pouvoir de dominer sur la vie qu'on lui attribue. Voyez HILEGIAU.
LIEU, terme de Pêche, sorte de poisson du genre des morues, et semblable aux éperlans, excepté qu'il est plus gros et plus ventru, et que sa peau est beaucoup plus noire. Cette pêche commence à Pâques, et finit à la fin de Juin, parce qu'alors les Pêcheurs s'équipent pour la pêche du congre ; ce sont les grands bateaux qui y sont employés ; la manœuvre de cette pêche est particulière ; il faut du vent pour y réussir, et que le bateau soit à la voîle ; on amorce les ains ou hameçons d'un morceau de peau d'anguille, en forme de petite sardine ; le lieu qui est fort vorace et goulu, n'a pas le temps par la dérive du bateau d'examiner l'appât et de le dévorer ; ainsi il sert à faire la pêche de plusieurs lieux.
On sale ce poisson pendant deux jours, après l'avoir dépouillé de sa tête et ouvert par le ventre. Deux fois vingt-quatre heures après on le retire du sel, on le lave dans l'eau de mer, et on l'expose à terre au soleil pendant plusieurs jours jusqu'à ce qu'il soit sec ; quand son apprêt est fini, on le met en grenier, et les Pêcheurs le viennent vendre à la saint Michel aux marchands d'Audierne qui l'achetent depuis sept jusqu'à dix livres le cent pesant ; ces derniers le mettent en paquets de deux quintaux pesant, et l'envaient ensuite à leur risque à Bordeaux en temps de foire.
Ce poisson au contraire du congre sec qui déperit continuellement par les mites qui le consomment, ne déperit point par la garde ; quand il est une fois bien sec, il augmente de poids par l'humidité ; la consommation s'en fait en France ; on prépare le lieu sec comme on fait la morue de même qualité.
Les Pêcheurs sont tous à la part ; le bateau, le maître et chaque matelot n'ont chacun également qu'un lot.
Ils ont de cinq principales espèces d'ains ; les plus gros semblables à ceux des Pêcheurs de Terre-neuve sur le Banc, servent à la pêche des congres et des posteaux ; les deuxiemes à prendre les lieux ; les troisiemes pour la pêche des vieilles ; les quatriemes hameçons ou claveaux servent à prendre des dorées, des plombs, et autres semblables poissons, dont les chairs servent de boite et d'appât aux claveaux, et les plus petits pour les moindres dorées qui servent aussi à boiter ; cette dernière sorte d'hameçons et plusieurs autres moindres servent pour le même usage.