S. f. terme de Mécanique, qui signifie la même chose que vibration ; c'est-à-dire le mouvement d'un pendule en descendant et en montant, ou, si on peut parler ainsi, sa descente et sa remontée consécutives et prises ensemble.

Axe d'oscillation est une ligne droite parallèle à l'horizon, qui passe, ou qui est supposée passer par le centre ou point fixe autour duquel le pendule oscille, et qui est perpendiculaire au plan où se fait l'oscillation. Voyez AXE.

Si on suspend un pendule simple entre deux demi-cycloïdes, dont les cercles générateurs aient leur diamètre égal à la moitié de la longueur du fil, toutes les oscillations de ce pendule, grandes et petites, seront isocrones, c'est-à-dire, se feront en temps égal. Voyez CYCLOÏDE et ISOCRONE.

Le temps d'une oscillation entière dans un arc de cycloïde quelconque est au temps de la descente perpendiculaire par le diamétre du cercle générateur, comme la circonférence du cercle est au diamétre.

Si deux pendules décrivent des arcs semblables, les temps de leurs oscillations seront en raison soudoublée de leurs longueurs.

Les nombres d'oscillations isocrones, faites par deux pendules dans le même temps sont entr'eux en raison inverse du temps que durent les oscillations prises séparément.

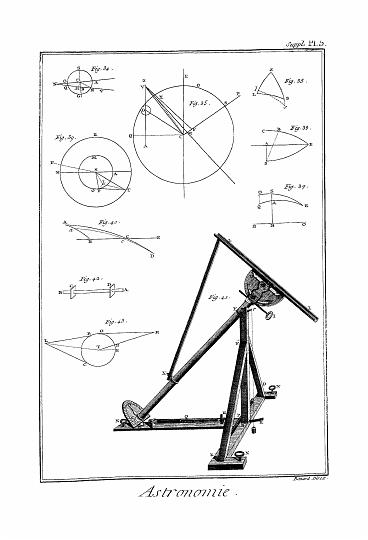
On trouve plus au long dans l'article PENDULE les lois du mouvement et des oscillations du pendule simple, c'est-à-dire, du pendule composé d'un seul poids A fort petit, et qu'on regarde comme un point, et d'une verge ou fil C A (fig. 36. Mécan.) dont on considère la pesanteur ou la masse comme nulle. Il est beaucoup plus difficîle de déterminer les lois d'un pendule composé, c'est-à-dire, les oscillations d'une verge B A (fig. 22.), que l'on regarde comme sans pesanteur et sans masse, et qui est chargée de plusieurs poids D, F, H, B ; il est certain que cette verge ne fait pas ses oscillations de la même manière que s'il n'y avait qu'un seul poids ; par exemple B, car supposons qu'il n'y ait en effet qu'un poids B, ce poids tendra à décrire la petite ligne B N au premier instant : or, s'il y avait d'autres poids en H, F, D, ces poids tendraient à décrire dans le même instant les lignes H M, F L, D K, égales à B N, de sorte que la portion D B de la verge devrait se trouver en K N ; et par conséquent la portion A D se trouverait dans la situation A K ; or cela ne se pourrait faire sans que la verge A D B se brisât en D ; et comme on la suppose inflexible, il est donc impossible que les poids B, H, F, D, décrivent les lignes B N, H M, F L, D K, etc. mais il faut que ces poids décrivent des lignes B C, H I, F G, D E, qui soient telles que la verge A D B conserve toujours sans se plier la forme d'une droite A E C. Or on peut imaginer un pendule simple d'une certaine longueur, qui fasse ses oscillations dans le temps que le pendule composé A D B fait les siennes. Ainsi la difficulté se réduit à trouver la longueur de ce pendule simple, et trouver la longueur de ce pendule simple, est la même chose que ce que les Géomètres appellent trouver le centre d'oscillation.

Le célèbre M. Huygens est le premier qui ait résolu ce problême dans son excellent ouvrage de horologio oscillatorio. Mais la méthode dont il s'est servi pour le résoudre, quoique bonne et exacte, était susceptible de quelques difficultés.

Toute la doctrine de ce grand géomètre sur le centre d'oscillation est fondée sur l'hypothèse suivante ; que le centre de gravité commun de plusieurs corps doit remonter à la même hauteur d'où il est tombé, soit que ces corps soient unis, ou separés l'un de l'autre en remontant, pourvu qu'ils commencent à remonter chacun avec la vitesse acquise par sa chute. Voyez CENTRE DE GRAVITE.

Cette hypothèse a été combattue par quelques auteurs, et regardée par d'autres comme fort douteuse. Ceux même qui convenaient de la vérité ne pouvaient s'empêcher de reconnaître qu'elle était trop hardie pour être admise sans preuve dans une science où l'on démontre tout.

Ce même principe a été démontré depuis par plusieurs géomètres, et il n'est autre chose que le fameux principe connu autrement sous le nom de conservation des forces vives, dont les Géomètres se sont servis depuis avec tant de succès dans la solution des problêmes de dynamique. Voyez DYNAMIQUE et FORCES VIVES.

Cependant, comme le principe de M. Huygens avait paru incertain et indirect à plusieurs géomètres ; ces considérations engagèrent M. Jacques Bernoulli, professeur de Mathématique à Bâle, mort en 1705, à chercher une solution du problême dont il s'agit. Il en trouva une assez simple, tirée de la nature du levier, et la fit paraitre dans les mémoires de l'Acad. des Sciences de Paris, année 1703. Après sa mort, son frère Jean Bernoulli fit imprimer dans les mémoires de la même académie, année 1714, une autre solution du même problême, encore plus facîle et plus simple. Nous ne devons point oublier de dire, qu'environ dans le même temps M. Taylor, célèbre géomètre anglais, trouva une solution à-peu près semblable à celle de M. Bernoulli, et la fit paraitre dans son livre intitulé methodus incrementorum ; ce qui fut le sujet d'une dispute entre les deux géomètres qui s'accusèrent réciproquement de s'être pillés. On peut voir les pièces de ce procès dans les actes de Leipsic de 1716 ; et dans les œuvres de M. Bernoulli, imprimées à Lausanne in -4°. en 1743. Quoi qu'il en sait, voici le précis de la théorie de M. Jean Bernoulli ; elle consiste en général à chercher d'abord quelle devrait être la gravité dans un pendule simple, de même longueur que le composé, pour que les deux pendules fissent leurs oscillations dans un temps égal. Il faut pour cela que le moment des deux pendules soit le même ; ensuite au-lieu de ce pendule simple d'une longueur connue, et d'une pesanteur supposée, M. Bernoulli substitue un pendule simple animé par la gravité naturelle, et il trouve aisément par une simple proportion la longueur que ce nouveau pendule doit avoir pour faire les vibrations en même temps que l'autre.

Quoique la méthode de M. Bernoulli soit assez simple, elle peut encore être simplifiée, même en faisant usage de son principe, comme je l'ai démontré dans mon traité de dynamique, l. II. c. IIIe probl. 1. et j'ai d'ailleurs donné en même temps une méthode particulière extrêmement simple pour résoudre ce problème. Voici une idée de cette méthode.

Il est certain que les corps B, H, F, D, ne pouvant décrire les lignes B N, H M, F L, D K, décrivent des lignes B C, H I, F G, D E, qui sont entr'elles comme les distances A B, A H, A F, A D, au point de suspension A ; d'où il s'ensuit que toute la difficulté se réduit à connaître une de ces lignes comme B C ; or au lieu de supposer que les corps B, H, F, D, tendent à se mouvoir avec les vitesses B N, H M, F L, D K, on peut supposer, ce qui revient au même, qu'ils tendent à se mouvoir avec les vitesses B C - C N, H I - I M, F G + G L, D E + E K, et comme de ces vitesses il ne reste que les vitesses B C, H I, F G, D E, il s'ensuit que si les corps B, H, F, D, n'avaient eu que les vitesses - C N, - I M, G L, E K, la verge A B serait demeurée en repos. Voyez DYNAMIQUE. Donc par la nature du levier on aura - B x C N x A B - H x I M x A H + F x G L x A F + D x E K x A D = 0. Or dans cette équation il n'y a qu'une seule inconnue, puisqu'en supposant B C donnée, tout le reste est donné ; on aura donc par cette équation la valeur de B C, et par le rapport de B C à E N, on connaitra le rapport de la vitesse du pendule composé à celle d'un pendule simple qui serait de la longueur de B A ; d'où il s'ensuit qu'on trouvera facilement la longueur du pendule simple isocrone au pendule composé ; en cherchant un pendule dont la longueur soit à A C comme B N est à B C. Voyez sur cela mon traité de dynamique, l. II. ch. IIIe probl. 1. vous y trouverez d'autres remarques curieuses sur le problême dont il s'agit ici.

Centre d'oscillation d'un pendule, est donc proprement, suivant ce qu'on vient de dire, un certain point pris dans ce pendule, prolongé, s'il est nécessaire, et dont chaque vibration se fait de la même manière que si ce point seul et isolé était suspendu à la distance où il est du point de suspension.

Ou bien, c'est un point tel, que si on y suppose ramassée toute la gravité du pendule composé, ses différentes oscillations se feront dans le même temps qu'auparavant.

Ainsi la distance de ce point au point de suspension est égale, comme on vient de le dire, à la longueur du pendule simple, dont les oscillations seraient isocrones à celle du corps suspendu. Voyez CENTRE. Chambers.

On appelle aussi en général oscillation le mouvement d'un corps qui Ve et vient alternativement en sens contraire comme un pendule. Ainsi, par exemple, un corps solide placé sur un fluide peut y faire des oscillations, lorsque ce solide n'est pas en repos parfait ; sur quoi voyez l'article FLOTTER. (O)

OSCILLATION, (Antiquité grecque et romaine) espèce de balancement que les anciens avaient imaginé pour donner une apparence de sépulture à ceux qui se défaisaient eux-mêmes ; car on croyait que leurs manes ne pouvaient jouir d'aucun repos, et l'on y remédiait par l'oscillation, qui consistait à attacher à une corde, une petite figure qui représentait le mort ; on balançait ensuite cette figure dans l'air, et enfin on lui faisait des funérailles. Dans le beau tableau de la prise de Troie par Polygnote, on voit, dit Pausanias, Ariadne assise sur une roche. Elle jette les yeux sur Phèdre sa sœur, qui, élevée de terre, et suspendue à une corde qu'elle tient des deux mains, semble se balancer dans les airs. C'est ainsi, continue l'historien, que le peintre a voulu couvrir le genre de mort, dont on dit que la malheureuse Phèdre finit ses jours. (D.J.)

OSCILLATION