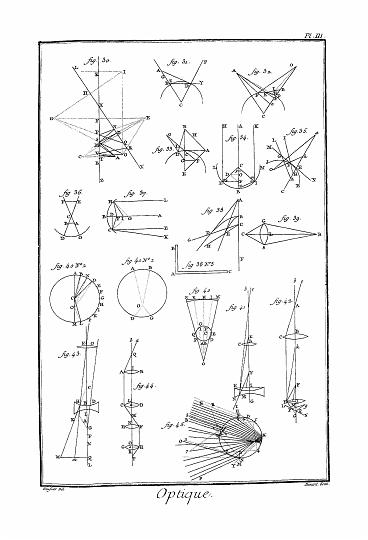
S. f. (Mécanique) est le nom que feu M. Bernoulli, professeur de Mathématique à Bâle, a donné à une courbe A B C (fig. 68. Mécan.) dont la propriété est telle qu'un corps qui tombe du point A, en vertu de sa pesanteur, le long de la concavité de cette courbe, arrive de A en B en moins de temps qu'il n'y arriverait, s'il descendait le long de toute autre courbe A D B, passant par les mêmes points A, B, ou même s'il descendait le long de la ligne droite A B.
Ce mot vient de deux mots grecs ; savoir, , superlatif de , qui signifie vite, prompt, et , temps. La courbe brachystochrone s'appelle aussi courbe ou ligne de la plus vite descente.
Feu M. Bernoulli proposa aux Géomètres en 1697, de déterminer quelle était cette courbe. Le problème fut résolu par M. Jacques Bernoulli son frère, alors professeur de Mathématique à Bâle, par M. Leibnitz, par M. le Marquis de l'Hôpital, et par M. Newton. M. Bernoulli avait averti les Géomètres dans son programme, que la ligne droite A B, passant par les deux points A, B, quoiqu'elle fût la plus courte de toutes celles qu'on pouvait faire passer par ces points, n'était pas néanmoins celle qu'un corps pesant, tombant de A, devait parcourir en moins de temps ; et en effet, on trouva que c'était une cycloïde, ou plutôt un arc de cycloïde passant par les points A, B, et dont le point A était l'origine. Voyez CYCLOÏDE.
Il n'est pas impossible de faire sentir à ceux même qui sont peu versés dans la Mécanique transcendante, comment il peut se faire que la ligne droite A B ne soit pas la ligne de la plus courte descente. Car, imaginons la ligne horizontale E C qui partage la courbe A B C en deux parties A C, C B, telles que la partie A C soit plus courte que A E, et la partie C B plus longue que E B ; il est certain que le corps A arrivera en C plutôt qu'il n'arriverait en E, puisqu'il aura moins de chemin à faire. Il est vrai qu'il emploiera ensuite plus de temps à parcourir C B, qu'il n'en mettra à parcourir E B ; mais il faut remarquer que les temps employés à parcourir les lignes A E, A C, C B, E B, ne sont point entr'eux comme ces lignes, parce que le corps ne les décrit pas d'un mouvement uniforme ; ainsi il ne doit pas paraitre impossible que l'excès du temps par A E sur le temps par A C, soit plus grand que l'excès du temps par C B sur le temps par E B. Ainsi de ce que la ligne droite A B est plus courte que la ligne courbe A C B, il ne s'ensuit nullement que la ligne droite A B doive être descendue en moins de temps que la ligne courbe A C B. L'espèce de raisonnement métaphysique que nous venons de faire, peut bien servir à faire soupçonner que la ligne de la plus vite descente peut être une courbe : mais ce raisonnement ne saurait jamais être une démonstration. C'est par le calcul seul qu'on peut s'assurer si ce qu'on a soupçonné est vrai, et le calcul démontre en effet qu'on a soupçonné juste. Voici à-peu-près comment on s'y prend pour déterminer la courbe de la plus vite descente. Sait A C B cette courbe, et ayant pris un arc infiniment petit C c, soit imaginé un arc quelconque infiniment petit C O c, terminé aux points C, c ; il est évident que le corps pesant arrivé en C, doit parcourir l'arc C c, en moins de temps que l'arc C O c. Car s'il était moins de temps à parcourir l'arc C O c, alors ce serait A C O c B, et non A C B qui serait la courbe de la plus vite descente, ce qui est contre l'hypothèse. Ainsi la propriété de la courbe dont il s'agit, est telle, qu'un de ses arcs quelconques infiniment petits C c, est parcouru en moins de temps que tout autre arc infiniment petit C O c, passant par les mêmes points C, c.
Maintenant soient imaginés les points infiniment proches C, c, et soit cherchée sur la ligne horizontale Q L, la position du point K, tel que C K c soit parcouru en moins de temps que tout autre chemin C k c, passant par C et c, on trouvera (Voyez REFRACTION) en menant les lignes K R, c r, perpendiculaires à Q L, que le sinus de l'angle C K R doit être au sinus de K c r, comme la vitesse le long de C K à la vitesse le long de K c : d'où il s'ensuit que la courbe cherchée doit être telle que le sinus de l'angle qu'un de ses côtés quelconque infiniment petit C K fait avec la verticale K R, soit proportionnel à la vitesse en K ; laquelle vitesse est comme la racine carrée de la hauteur d'où le corps est parti. Or en achevant le calcul, on trouve que cette propriété convient à la cycloïde. Voyez CYCLOÏDE.
Si l'on supposait qu'un corpuscule de lumière traversât l'atmosphère, de manière qu'il arrivât d'un point à un autre dans le plus court temps possible, la courbe qu'il décrirait serait une brachystochrone, pourvu que l'on fit certaines hypothèses sur la densité du milieu. Voyez REFRACTION, ACTION, CAUSES FINALES.
Voyez dans les Mémoires de l'Académie de 1718. deux solutions du problème de la brachystochrone, données par M. Bernoulli, et toutes deux fort simples. Galilée a cru faussement que la brachystochrone était un arc de cercle. La Géométrie de son temps n'était pas encore assez avancée pour résoudre ce problème. On trouve dans le second volume de la Mécanique de M. Euler, imprimé à Petersbourg 1736. une solution très-élegante de ces problèmes et des théorèmes fort simples et fort généraux sur les propriétés de la brachystochrone ; la solution du problème devient beaucoup plus difficîle lorsqu'on suppose que le corps se meut dans un milieu résistant, parce qu'alors la vitesse ne dépend pas de la hauteur seule. M. Euler a donné aussi la brachystochrone pour ce cas-là, ce que personne n'avait encore fait avant lui. (O)
Articles populaires Science
VARIABLE
adj. (Algèbre et Géométrie) on appelle quantités variables en Géométrie, les quantités qui varient suivant une loi quelconque. Telles sont les abscisses et les ordonnées des courbes, leurs rayons osculateurs, etc.On les appelle ainsi par opposition aux quantités constantes, qui sont celles qui ne changent point, comme le diamètre d'un cercle, le paramètre d'une parabole, etc.
On exprime communément les variables par les dernières lettres de l'alphabet Xe y, z.
Quelques auteurs au-lieu de se servir de l'expression de quantités variables, disent des fluentes. Voyez FLUENTE et FLUXION.
Lire la suite...