S. f. (Géométrie) se dit en général de l'élévation d'un corps au-dessus de la surface de la terre, ou au-dessus d'un plan quelconque.
C'est dans ce sens qu'on dit qu'un oiseau vole à une grande hauteur, que les nuées sont à une grande hauteur.
HAUTEUR, se dit aussi de la dimension d'un corps estimée dans un sens perpendiculaire à la surface de la terre. C'est dans ce sens, qu'on dit qu'un mur a beaucoup de hauteur.
HAUTEUR, en Astronomie, est la même chose qu'élévation. Ainsi on dit la hauteur du pôle, la hauteur de l'équateur. Voyez ÉLEVATION.
Prendre hauteur, terme dont se servent les Marins, et qui signifie mesurer la hauteur du Soleil sur l'horizon ; c'est principalement à midi que l'on prend hauteur en mer. Les Marins se servent pour cela de différents instruments ; l'arbalestrille, le quartier anglais, l'octant, etc. Voyez ARBALESTRILLE, QUARTIER ANGLOIS, OCTANT. Voyez aussi le Traité de Navigation de M. Bouguer. (E)
Hauteur d'une figure, en Géométrie, est la distance de son sommet à sa base, ou la longueur d'une perpendiculaire abaissée du sommet sur la base. Voyez FIGURE, BASE et SOMMET.
Ainsi K L (Planche I. Géom. fig. 19.) étant prise pour la base d'un triangle rectangle K L M, la perpendiculaire K M sera la hauteur de ce triangle.
Des triangles qui ont des bases et des hauteurs égales, sont égaux en surface ; et les parallélogrammes sont doubles des triangles de même base et de même hauteur. Voyez TRIANGLE, PARALLELOGRAMME, etc.
Hauteur, en Optique, se dit ordinairement de l'angle compris entre une ligne tirée par le centre de l'oeil parallélement à l'horizon, et un rayon visuel qui vient de l'objet à l'oeil.
Si par les deux extrémités S T, d'un objet, (Pl. d'Opt. fig. 13.) on tire deux parallèles T V, et S Q, l'angle T V S, intercepté entre un rayon qui passe par le sommet S, et qui en termine l'ombre en V, est appelé par quelques auteurs la hauteur du lumineux.
Il y a trois moyens de mesurer les hauteurs ; on peut le faire géométriquement, trigonométriquement, et par l'optique. Le premier moyen est un peu indirect, et demande peu d'apprêt ; le second se fait avec le secours d'instruments destinés à cet usage, et le troisième par les ombres.
Les instruments dont on fait principalement usage pour mesurer les hauteurs, sont le quart de cercle, le graphomètre, etc. Voyez-en les descriptions ou les applications à leurs articles respectifs, QUART DE CERCLE, GRAPHOMETRE, etc.
Prendre des hauteurs accessibles. Pour mesurer géométriquement une hauteur accessible, supposons qu'il s'agisse de trouver la hauteur A B, (Pl. Géom. fig. 88.) plantez un piquet D E perpendiculairement à la surface de la terre, assez long pour monter à la hauteur de l'oeil ; étendez-vous ensuite par terre, les pieds contre le piquet ; si les points E B, se trouvent dans la même ligne droite avec l'oeil C ; la longueur C A est égale à la hauteur A B ; si quelqu'autre point plus bas, comme F, se trouve dans la même ligne que le point E, et l'oeil, approchez le piquet de l'objet : au contraire, si la ligne menée de l'oeil par le point E, rencontre quelque point au-dessus de la hauteur cherchée, il faut éloigner le piquet jusqu'à ce que la ligne C E rase le vrai point que l'on demande. Alors mesurant la distance de l'oeil C au pied de l'objet A, on a la véritable hauteur cherchée, puisque C A = A B.
Ou bien opérez de la manière suivante. A la distance de trente ou quarante pieds, ou même plus, plantez un piquet D E (fig. 89.) et à la distance de ce piquet au point C, plantez-en un autre plus court, de manière que l'oeil étant en F, les points E B, puissent être dans la même ligne droite avec F ; mesurez la distance entre les deux piquets G F, et la distance entre le plus court piquet et l'objet H F, de même que la différence des hauteurs des piquets G E ; aux lignes G F, G E, H F ; cherchez une quatrième proportionelle B H, ajoutez-y la hauteur du plus court piquet F C, la somme est la hauteur cherchée A B.
Mesurer une hauteur accessible trigonométriquement. Supposons qu'il s'agisse de trouver la hauteur A B, (Pl. Trigon. fig. 23.) choisissez une station en E, et avec un quart de cercle, un graphomètre, ou un autre instrument gradué et disposé d'une manière convenable, déterminez la quantité de l'angle de hauteur A D C. Voyez ANGLE.
Mesurer la plus petite distance du point de station à l'objet, savoir D C, qui est par conséquent perpendiculaire à A C. Voyez DISTANCE.
Maintenant C étant un angle droit, il est aisé de trouver la ligne A C, puisque dans le triangle A C D, nous avons les deux angles C D, et un côté C D opposé à l'un de ces angles ; pour trouver le côté opposé à l'autre angle, l'on fera cette proportion : le sinus de l'angle A est au côté donné D C, opposé à cet angle, comme le sinus de l'autre angle D est au côté cherché C A. Voyez TRIANGLE.
A ce côté ainsi déterminé, ajoutez B C, la somme est la hauteur perpendiculaire demandée.
L'opération se fait plus commodément par les logarithmes. Voyez LOGARITHME.
Si l'on commet quelqu'erreur, en prenant la quantité de l'angle A, (fig. 24.) la véritable hauteur B D sera à la fausse B C, comme la tangente de l'angle véritable D A B, est à la tangente de l'angle erroné C A B.
Ainsi les erreurs de cette nature seront plus considérables dans une grande hauteur que dans une moindre.
Il suit aussi que l'erreur est plus grande, quand l'angle est plus petit que lorsqu'il est plus grand. Pour éviter ces inconvéniens, il faut choisir une station à une distance moyenne, de manière que l'angle de hauteur D E B, soit à-peu-près la moitié d'un angle droit.
Pour mesurer une hauteur accessible avec le secours de l'optique, et par l'ombre du corps. Voyez OMBRE.
Mesurer une hauteur accessible par le carré géométrique. Supposons que l'on demande de trouver la hauteur A B, (Pl. géom. fig. 90.) choisissant une station à volonté en D, et mesurant sa distance à l'objet D B, faites tourner le carré çà et là, jusqu'à ce que vous aperceviez par les pinnules le haut de la tour A ; alors si le fil coupe l'ombre droite, dites : la partie de l'ombre droite coupée est au côté du carré, comme la distance de la station D B, est à la partie de la hauteur A E. Si le fil coupe l'ombre verse, dites : le côté du carré est à la partie de l'ombre verse coupée, comme la distance de la station D B, est à la partie de la hauteur A E.
Ainsi ayant trouvé A E, dans l'un et l'autre cas, par la règle de trois, si l'on y ajoute la partie de la hauteur B E, cette somme est la hauteur que l'on demande.
Mesurer géométriquement une hauteur inaccessible. Supposons qu'A B, (fig. 89.) soit une hauteur inaccessible, telle qu'on ne puisse pas appliquer une mesure jusqu'à son pied ; trouvez la distance C A, ou F H, ainsi qu'on l'a enseigné à l'article DISTANCE, et procédez dans tout le reste, comme l'on a fait par rapport aux distances accessibles.
Mesurer trigonométriquement une hauteur inaccessible. Chaisissez deux stations G, E, (Pl. trigon. fig. 25.) qui soient dans la même ligne droite que la hauteur A B, cherchée ; et à une distance D F, l'une de l'autre, telle que l'angle F A D ne soit point trop petit, ni l'autre station G trop près de l'objet A B, prenez avec un instrument convenable la quantité des angles A D C, A F C, et C F B. Voyez ANGLE ; mesurez aussi l'intervalle F D.
Alors dans le triangle A F D, on a l'angle D donné par l'observation, et l'angle A F D, en soustrayant l'angle observé A F C, de la somme de deux angles droits ; et par conséquent le troisième angle D A F, en soustrayant les deux autres de la valeur de deux angles droits : on a aussi le côté F D, d'où l'on détermine le côté A F, par la règle exposée ci-dessus, lorsqu'il était question du problème des hauteurs accessibles. De plus, dans le triangle A C F, ayant un angle droit C, un angle F observé, et un côté A F, on trouvera par la même règle le côté A C, et l'autre côté C F. Enfin, dans le triangle F C B, ayant un angle droit C, l'angle observé C F B, et un côté C F ; la même règle fera découvrir l'autre côté C B.
C'est pourquoi ajoutant A C, et C B, la somme est la hauteur cherchée A B.
Trouver une hauteur inaccessible par le moyen de l'ombre ou du carré géométrique. Chaisissez deux stations en D H, (Pl. géom. fig. 90.) et trouvez la distance D H ou C G, observez quelle partie de l'ombre droite ou verse est coupée par le fil.
Si les ombres droites sont coupées dans les deux stations, dites : la différence des ombres droites dans les deux stations est au côté du carré, comme la distance des stations G C est à la hauteur E A. Si le fil coupe l'ombre verse aux deux stations, dites : la différence des ombres verses marquées aux deux stations est à la plus petite ombre verse, comme la distance des stations C G est à l'intervalle G E ; cela étant connu, on trouve aussi la hauteur E B, par le moyen de l'ombre verse en G, comme dans le problème pour les hauteurs accessibles. Enfin, si le fil dans la première station G, coupe les ombres droites, et que dans la dernière, il coupe les ombres verses, dites : comme la différence du produit de l'ombre droite par l'ombre verse soustraite du carré du côté du carré géométrique, est au produit du côté de ce carré par l'ombre verse ; ainsi la distance des stations G C, est à la hauteur cherchée A E.
Etant donnée la plus grande distance à laquelle un objet peut être vu, trouver sa hauteur. Supposons la distance D B, (Pl. géograp. fig. 9.) réduisez-la en degrés ; par ce moyen vous aurez la quantité de l'angle C : de la sécante de cet angle ôtez le sinus total B C, le reste sera A B en parties, dont B C, en contient 10000000. dites ensuite : 10000000. est à la valeur d'A B, en mêmes parties, comme le demi-diamètre de la terre BC 19695539. est à la valeur de la hauteur AB, en pieds de Paris.
Supposons, par exemple, que l'on demande la hauteur d'une tour A B, dont le sommet est visible à la distance de cinq milles ; alors D C B, sera de 20'. Si l'on soustrait le sinus total 10000000. de la secante 10000168. de cet angle, le reste A B est 168. que l'on trouvera de 331. pieds de Paris.
La hauteur de l'oeil dans la perspective, est une ligne droite qui tombe de l'oeil perpendiculairement au plan géométral.
La hauteur d'une étoîle ou d'un autre point, est proprement un arc d'un cercle vertical, intercepté entre ce point et l'horizon. Voyez VERTICAL. Delà vient :
Hauteur méridienne ; le méridien étant au cercle vertical, une hauteur méridienne, c'est-à-dire la hauteur d'un point dans le méridien, est un arc du méridien intercepté entre ce point et l'horizon. Voyez MERIDIEN.
Pour observer la hauteur méridienne du Soleil, d'une étoile, ou de tout autre phénomène, par le moyen du quart de cercle. Voyez MERIDIEN.
Pour observer une hauteur méridienne avec un gnomon. Voyez GNOMON.
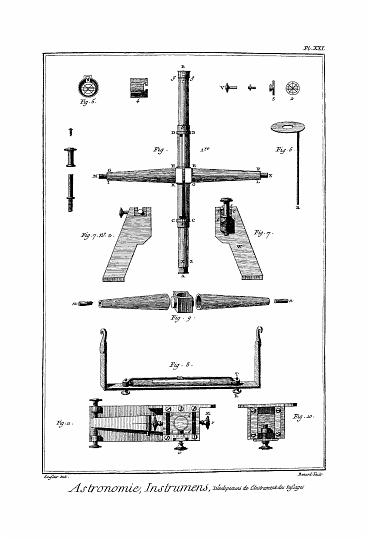
Vous pourrez aussi trouver la hauteur du Soleil sans le secours du quart de cercle ou de tout autre instrument semblable, en élevant perpendiculairement au point C, par exemple un stîle ou un fil d'archal (Pl. astrom. fig. 62.) et en décrivant du centre C l'arc A F, quatrième partie d'une circonférence, faites C E égale à la hauteur du style, et par E tirez E D, parallèle à C A, que vous ferez égale à la longueur de l'ombre ; si vous mettez ensuite une règle de C en D, elle coupera le quart de cercle en B ; et B A est l'arc de la hauteur du Soleil.
HAUTEUR des eaux, (Hydraulique) voyez ÉLEVATION. (K)
HAUTEUR, (Grammaire Morale) Si hautain est toujours pris en mal, hauteur est tantôt une bonne, tantôt une mauvaise qualité, selon la place qu'on tient, l'occasion où l'on se trouve, et ceux avec qui l'on traite. Le plus bel exemple d'une hauteur noble et bien placée est celui de Popilius qui trace un cercle autour d'un puissant roi de Syrie, et lui dit : vous ne sortirez pas de ce cercle sans satisfaire à la république, ou sans attirer sa vengeance. Un particulier qui en userait ainsi serait un impudent ; Popilius qui représentait Rome, mettait toute la grandeur de Rome dans son procédé, et pouvait être un homme modeste.
Il y a des hauteurs généreuses ; et le lecteur dira que ce sont les plus estimables. Le duc d'Orléans régent du royaume, pressé par M. Sum, envoyé de Pologne, de ne point recevoir le roi Stanislas, lui répondit : dites à votre maître que la France a toujours été l'asîle des rais.
La hauteur avec laquelle Louis XIV. traita quelquefois ses ennemis, est d'un autre genre, et moins sublime. On ne peut s'empêcher de remarquer ici, que le père Bouhours dit du ministre d'Etat Pompone ; il avait une hauteur, une fermeté d'ame, que rien ne faisait ployer. Louis XIV. dans un mémoire de sa main, (qu'on trouve dans le siècle de Louis XIV.) dit de ce même ministre, qu'il n'avait ni fermeté ni dignité. On a souvent employé au pluriel le mot hauteur dans le style relevé ; les hauteurs de l'esprit humain ; et on dit dans le style simple, il a eu des hauteurs, il s'est fait des ennemis par ses hauteurs.
Ceux qui ont approfondi le cœur humain en diront davantage sur ce petit article.
HAUTEUR, terme d'Architecture. On dit qu'un bâtiment est arrivé à hauteur, lorsque les dernières assises sont posées pour recevoir la charpente. On dit aussi hauteur d'appui, pour signifier trois pieds de haut : et hauteur de marche, six pouces, parce que l'usage a déterminé ces hauteurs.
HAUTEUR, se dit dans l'Art militaire, du nombre de rangs sur lesquels une troupe est formée, ou ce qui est la même chose, du nombre d'hommes dont les files sont composées. Voyez FILE.
Ainsi, dire qu'une troupe est formée à deux ou trois de hauteur, etc. c'est dire qu'elle a deux ou trois rangs, ou deux ou trois hommes, etc. dans chaque file. Voyez ÉVOLUTIONS.
Hauteur, se dit aussi dans la marche des troupes de la ligne qui termine la tête du côté de l'ennemi. Lorsque l'armée est en marche pour combattre, toutes les colomnes doivent marcher à la même hauteur, c'est-à-dire que la tête de chaque colomne doit être également avancée vers l'ennemi. Voyez MARCHE. (Q)
HAUTEURS, en termes de guerre, signifient les éminences qui se trouvent autour d'une place fortifiée, et où les ennemis ont coutume de prendre poste. Dans ce sens, on dit que l'ennemi s'est emparé des hauteurs, qu'il parait sur les hauteurs, etc. Chambers.
HAUTEUR, (Géographie) ce mot qui signifie élévation, a plusieurs usages dans la Géographie.
On dit qu'un château est sur la hauteur, sur une hauteur, lorsqu'il est élevé sur une colline, et commande une ville ou un bourg, qui est au pied, ou sur le penchant.
On dit en termes de navigation : quand nous fumes à la hauteur d'un tel port, pour dire vis-à-vis.
On dit en termes de Géographie astronomique, la hauteur ou l'élévation du pôle, pour désigner la latitude ; car quoique la hauteur du pôle et la latitude soient des espaces du ciel dans des parties différentes, ces espaces sont pourtant tellement égaux, que la détermination de l'un ou de l'autre produit le même effet et la même connaissance, parce que la hauteur du pôle est l'arc du méridien compris entre le pôle et l'horizon ; et la latitude du lieu est l'arc de ce même méridien, compris entre le zénith du lieu et l'équateur. Or à mesure que le pôle dont on examine la hauteur s'élève de l'horizon, autant l'équateur s'éloigne du zénith du lieu, puisqu'il y a toujours 90 degrés de l'un à l'autre. Ainsi l'observatoire de Paris où la hauteur du pôle est de 48d. 50'. 10''. a son zénith à pareille distance de l'équateur. On dit prendre hauteur, pour dire mesurer la distance d'un astre à l'horizon.
La hauteur de l'équateur est l'arc du méridien compris entre l'horizon et l'équateur ; elle est toujours égale au complément de la hauteur du pôle, c'est-à dire à ce qui manque à la hauteur du pôle, pour être de 90 degrés ; la raison en est facile, par le principe que nous avons établi, que du pôle à l'équateur, la distance est invariablement de 90 degrés, si le pôle s'éleve, l'équateur s'abaisse : si le pôle s'abaisse, l'équateur s'élève à son tour. Plus le pôle est élevé, plus sa distance au zénith est diminuée, et de même l'horizon s'est abaissé, et sa distance à l'horizon est plus petite dans la même proportion.
La hauteur de l'équateur se peut connaître de jour, par le moyen de la hauteur du Soleil ; on la trouve facilement avec un quart de cercle bien divisé, ou avec quelqu'autre instrument astronomique, ainsi que par le moyen de la déclinaison, que l'on peut connaître par la trigonométrie sphérique, après que l'on a supputé par les tables astronomiques, le véritable lieu dans le zodiaque. Voyez ÉQUATEUR. (D.J.)
HAUTEUR des caractères d'Imprimerie, (Fonderie en Caracteres) on entend par la hauteur dite en papier, la distance du corps sur lequel ils sont fondus, depuis le pied qui sert d'appui à la lettre, jusqu'à l'autre extrémité où est l'oeil. Cette hauteur est fixée sagement par les édits du roi et règlements de la Librairie, à dix lignes et demie géométriques, pour éviter la confusion que des différentes hauteurs causeraient dans l'Imprimerie ; cette hauteur n'est pas de même par-tout : on distingue la hauteur d'Hollande qui a près d'une ligne de plus qu'à Paris ; celles de Francfort, de Flandres, et même de Lyon, ont plus de dix lignes. Voyez OEIL.
HAUTEUR, (mettre à) en terme de Raffineur ; c'est l'action de verser la cuite dans les formes à-peu-près à la même hauteur ; savoir de deux pouces loin du bord dans les petites, et dans les autres à proportion de leur grandeur. On met à hauteur, afin qu'en achevant d'emplir les formes, le fond de la chaudière où le grain est tombé, soit également partagé dans toutes.
Articles populaires Science
HOMOCENTRIQUE
adj. terme d'Astronomie, il signifie la même chose que concentrique ; mais ce dernier mot est plus en usage. Voyez CONCENTRIQUE.Lire la suite...