S. m. en terme de Géométrie, c'est une figure comprise entre trois lignes ou côtés, et qui par conséquent a trois angles. Voyez FIGURE et ANGLE.
Si les trois lignes ou côtés d'un triangle sont des lignes droites, on l'appelle triangle rectiligne. Voyez RECTILIGNE.
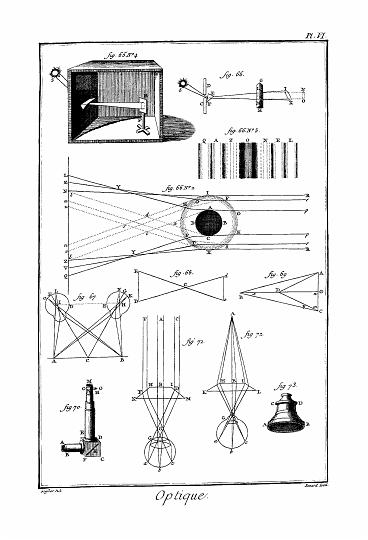
Si les trois côtés du triangle A B C, Planche de Géométrie, fig. 68. sont égaux, on l'appelle triangle équilatéral. Voyez ÉQUILATERAL.
S'il n'y a que deux de ses côtés égaux, comme D E F, fig. 69. on l'appelle triangle isoscele ou équicrural. Voyez ISOSCELE.
Si tous les côtés sont inégaux entr'eux, comme A C B, fig. 70. on l'appelle triangle scalene. Voyez SCALENE.
Si un des angles K d'un triangle K M L, fig. 71. est droit, on dit que le triangle est rectangle. Voyez RECTANGLE.
Si un des angles N, fig. 72. est obtus, on dit que le triangle est obtusangle, ou amblygone. Voyez AMBLYGONE.
Si les trois angles sont aigus, comme ACB, fig. 68. le triangle s'appelle acutangle ou oxygone. Voyez ACUTANGLE, etc.
Si les trois lignes du triangle sont courbes, on l'appelle curviligne. Voyez CURVILIGNE.
Si quelque côté du triangle est droit et les autres courbes, on l'appelle triangle mixtiligne.
Si tous les côtés sont des arcs de grands cercles ou de sphère, le triangle s'appelle sphérique. Voyez SPHERIQUE.
Constructions de triangles. 1°. Deux côtés A B, A C, fig. 73. ayant été donnés en nombres ou autrement, aussi-bien que la quantité de l'angle A compris entre ces côtés. Pour en construire un triangle, prenez A B pour la base ; et en A, formez l'angle donné pour l'autre jambe, tracez l'autre ligne donnée A C, enfin tirez la ligne B C, et pour-lors A B C sera le triangle que l'on cherche.
D'où il suit qu'ayant déterminé deux côtés avec l'angle compris entr'eux, vous avez déterminé tout le triangle ; par conséquent si en deux angles A C B et a c b, a = A, et que l'on ait a b : a c : : A B : A C, alors les triangles sont déterminés de la même manière, et par conséquent ils sont semblables ; ainsi c. = C ; b = B, et a b : b c : : A B : B C. etc.
2°. Trais côtés A B, B C et C A, fig. 68. étant donnés, dont deux, comme A C et A B pris ensemble, sont plus grands que le troisième ; si vous voulez en construire un triangle, prenez A B pour la base, et du point A avec l'intervalle A C, décrivez un arc y ; et du point B avec l'intervalle B C, décrivez un autre arc x : tirez les lignes droites A C et B C, vous aurez le triangle.
Il ne faut pas s'imaginer que ce problème soit toujours possible ; dès-là que la somme des deux côtés est plus grande que le côté pris pour base, ainsi que tous les auteurs qui ont écrit sur la Géométrie paraissent en être persuadés ; car, prenant toujours A B pour base, si le côté A C, par exemple, surpassait cette base d'une quantité égale ou plus grande que l'autre côté B C, l'intersection ne pourrait pas se faire, et par conséquent la construction ne serait pas possible. Il est donc nécessaire, quand on propose ce problème, d'y mettre plus de condition qu'on n'a de coutume, de peur que l'on ne tombe dans une construction absurde, comme je l'ai Ve arriver.
C'est pourquoi, comme on ne peut construire qu'un triangle avec trois lignes droites données, il s'ensuit qu'en déterminant les trois côtés, tout le triangle est déterminé.
Ainsi si en deux triangles A C B et a c b, fig. 73. l'on a A C ; A B : : a c : a b ; A C : C B : : a c : b c ; alors les triangles sont déterminés de la même manière, par conséquent ils sont semblables et équiangles.
3°. Une ligne droite comme A B, et les deux angles A et B adjacens, lesquels pris ensemble sont moindres que deux angles droits, étant donnés ; pour décrire le triangle A B C aux extrémités de la ligne donnée A B, formez les deux angles donnés A et B : continuez les côtés A C et B C, jusqu'à ce qu'ils se rencontrent en C. alors vous aurez le triangle A B C que vous cherchiez.
Desorte qu'un côté et deux angles étant donnés, on a tout le triangle ; par conséquent, si deux triangles A = a et B = b ; alors ces triangles seront déterminés de la même manière, et par conséquent semblables.
Manière de mesurer les triangles. Pour trouver la superficie d'un triangle, multipliez la base A B, fig. 74. par la hauteur C d, la moitié du produit est la superficie du triangle A B C.
Ou de cette autre manière : multipliez la moitié de la base A B par la hauteur C d, ou toute la base par la moitié de la hauteur, le produit vous donnera la superficie du triangle.
Ou bien on trouve la superficie d'un triangle en joignant ensemble les trois côtés, et prenant la moitié de la somme, et de cette moitié on soustrait chaque côté séparément ; après quoi on multiplie la moitié de cette somme par le produit des trois restes, et l'on tire la racine carrée de ce dernier produit ; d'où il suit, 1°. que si entre la base et la moitié de la hauteur, ou entre la hauteur et la moitié de la base, on trouve une moyenne proportionnelle, ce sera le côté d'un carré égal au triangle. 2°. Si la superficie d'un triangle est divisée par la moitié de la base, le quotient est la hauteur.
Propriétés des triangles plans. 1°. Si en deux triangles A B C, a b c, fig. 73. l'angle A = a les côtés A B = a b et A C + a c, alors le côté B C = b c et les angles C = c et B = b, et par conséquent ces triangles seront égaux et semblables.
2°. Si un côté du triangle A B C, fig. 75. est continué jusqu'à D, l'angle extérieur D A B sera plus grand qu'aucun des deux angles intérieurs opposés B ou C.
3°. Dans chaque triangle, le plus grand côté est opposé au plus grand angle, et le plus petit côté au plus petit angle.
4°. Dans tous les triangles, deux côtés tels qu'ils soient, sont plus grands que le troisième.
5°. Si en deux triangles les différents côtés de l'un sont respectivement égaux aux côtés de l'autre, les angles seront aussi respectivement égaux, et par conséquent les triangles seront entièrement égaux et semblables.
6°. Si quelque côté, comme B C, fig. 76. d'un triangle A C B, est continué jusqu'à D, l'angle extérieur D O A sera égal aux deux angles intérieurs opposés, y et z pris ensemble.
7°. En tout triangle, comme A B C, les trois angles A, B, C, pris ensemble, sont égaux à deux angles droits, ou à 180d. d'où il s'ensuit, 1°. que si le triangle est rectangle, comme M K L, fig. 71. les deux angles obliques M et L pris ensemble, font un angle droit ou 90d. et par conséquent ce sont des demi-angles droits, si le triangle est isoscele. 2°. Si un angle d'un triangle est oblique, les deux autres pris ensemble sont pareillement obliques. 3°. Dans un triangle équilatéral, chaque angle est de 60 degrés. 4°. Si un angle d'un triangle est soustrait de 180d. le restant est la somme des deux autres ; et si la somme de deux angles est soustraite de 180d. le restant est le troisième angle. 5°. Si deux angles d'un triangle sont égaux à deux angles d'un autre triangle, soit conjointement, soit séparément, le troisième angle de l'un est égal au troisième angle de l'autre. 6°. Comme dans un triangle isoscele D F E, fig. 69. les angles de la base y et u sont égaux ; si l'angle d'en-haut est soustrait de 180d. et que le restant soit divisé par 2, le quotient est la quantité de chacun des angles égaux ; de même si le double d'un des angles de la base y est soustrait de 180d. le restant est la quantité de l'angle d'en-haut.
8°. Si en deux triangles A B C et a b c, fig. 73. A B. = a b., A = a, et B = b, alors A C. = a c. B C. = b c. C = c et le triangle A C B = a c b. d'où il s'ensuit que si en deux triangles A C B. et a c b, A = a, B = b, et B C = b c ; alors C = c, par conséquent A C = a c, A B = a b et le triangle A C B = a c b.
9°. Si dans un triangle D F E les angles de la base y et u, fig. 69. sont égaux, le triangle est isoscele : par conséquent si les trois angles sont égaux, le triangle est équilatéral.
10°. Si dans un triangle A B C une ligne droite est tirée parallèlement à la base, elle coupe les côtés proportionnellement, et forme un petit triangle semblable au grand.
11°. Tout triangle peut être inscrit dans un cercle. Voyez CERCLE.
12°. Le côté d'un triangle équilatéral inscrit dans un cercle, est en puissance triple du rayon. Voyez RAYON.
13°. Les triangles de même base et même hauteur, c'est-à-dire, qui se trouvent entre les mêmes lignes parallèles, sont égaux. Voyez PARALLELE.
14°. Tout triangle, comme C F D, (fig. 41.) est la moitié d'un parallélogramme A C D B, de même ou d'égale base C D, et de même hauteur, ou entre les mêmes parallèles : ou bien un triangle est égal à un parallélogramme qui est sur la même base, mais qui n'a que la moitié de la hauteur, ou qui n'ayant que la moitié de la base, a la même hauteur que le triangle. Voyez PARALLELOGRAMME.
15°. Dans tous les triangles tant plans que sphériques, les côtés sont proportionnels aux sinus des angles opposés.
16°. Dans tous les triangles plans, la somme des deux côtés est à leur différence, comme la tangente de la moitié de la somme des angles opposés est à la tangente de la moitié de leur différence.
17°. Si l'on fait tomber une perpendiculaire sur la base d'un triangle obliquangle, la différence des carrés des côtés est égale au double du rectangle sous la base et la distance qu'il y a de la perpendiculaire au milieu de la base.
18°. Les côtés d'un triangle sont coupés proportionnellement, par une ligne qu'on tire parallélement à la base.
19°. Un triangle entier est à un triangle coupé par une ligne droite, comme le rectangle sous les côtés coupés est au rectangle des deux autres côtés.
20°. Dans un triangle rectiligne une ligne de l'angle droit perpendiculairement sur l'hypothenuse, divise le triangle en deux autres triangles rectilignes, lesquels sont semblables au premier triangle, et l'un à l'autre.
21°. En tout triangle rectangle le carré de l'hypothenuse est égal à la somme des carrés des deux autres côtés. Voyez HYPOTHENUSE.
22°. Si quelqu'angle d'un triangle est coupé en deux parties égales, la ligne qui le coupe divisera le côté opposé proportionnellement aux côtés qui forment cet angle. Voyez BISSECTION.
23°. Si l'angle du sommet de quelque triangle est coupé en deux parties égales, la différence des rectangles faits par les côtés et par les segments de la base, est égale au carré de la ligne qui coupe l'angle en deux.
24°. Si une ligne droite B E (fig. 78.) coupe en deux un angle A B C d'un triangle, le carré de ladite ligne B E = A B + B C - A E + E C. Newton, arith. univers.
Pour diviser un triangle dans un certain nombre donné de parties égales, divisez la base C D (fig. 77.) en autant de parties égales qu'il s'agit de diviser la figure, et tirez les lignes A 1, A 2, etc.
Sur les propriétés des triangles sphériques. Voyez SPHERIQUE.
TRIANGLE, en terme de Trigonométrie. La solution ou analyse des triangles est du ressort de la trigonométrie. Voyez les figures de TRIGONOMETRIE.
Les différents cas peuvent être réduits aux problèmes suivants.
Solution des triangles plans. 1°. Deux angles A et C (tabl. trigon. fig. 26.) étant donnés conjointement avec le côté A B, opposé à l'un de ces deux angles C ; pour trouver le côté B C, opposé à l'autre angle A, en voici la règle : le sinus de l'angle C est au côté donné A B, qui lui est opposé, comme le sinus de l'autre angle A est au côté que l'on cherche.
C'est pourquoi le côté B C se trouve aisément par les logarithmes ou par la règle de trois ou de proportion. Voyez LOGARITHME.
Car par exemple, supposez C = 48d. 35'. A = 57d. 28'. A B = 74'. l'opération se fait de cette manière.
Le nombre qui répond à cela dans la table des logarithmes est 83, qui est la quantité du côté que l'on cherchait.
2°. Deux côtés A B et B C, ayant été donnés conjointement avec l'angle C, opposé à l'un des deux, pour trouver les autres angles A et B, voici la règle : un côté A B est au sinus de l'angle donné C, et opposé à ce côté, comme l'autre côté B C est au sinus de l'angle opposé que l'on cherche.
Le nombre qui répond à cela dans la table des logarithmes est 61d. 37'. et comme l'angle donné C est de 72°. 15'. la somme des deux autres 133°. 52'. étant soustraite de 180, total des trois, vous aurez 46°. 8'pour l'autre angle B que vous cherchiez.
De même supposez que dans un triangle rectangle (fig. 28.) outre l'angle droit A on ait donné l'hypothenuse B C = 49, et la cathète A C = 36 pour trouver l'angle B, voici comme on opere.
Le nombre qui répond à cela dans la table des logarithmes est 47°. 16'. par conséquent C = 42°. 44'.
3°. Deux côtés B A et A C, et l'angle A compris entre ces côtés étant donnés, pour trouver les deux autres angles.
I. Si le triangle A B C est rectangle, prenez un des côtés, qui forment l'angle droit, comme A B, pour rayon, pour lors C A sera la tangente de l'angle opposé B, en ce cas la règle est qu'un côté A B est à l'autre A C, comme le sinus total est à la tangente de l'angle B.
Le nombre qui répond à cela, dans la table des logarithmes, est 34°. 21'. par conséquent l'angle C est de 55°. 39'.
II. Si l'angle A est oblique (fig. 26.), il faut faire cette proportion, la somme des côtés donnés A B et A C est à leur différence, comme la tangente de la moitié de la somme des angles cherchés C et B est à la tangente de la moitié de leur différence : c'est pourquoi en ajoutant la moitié de la différence à la moitié de la somme, ce total donnera le plus grand angle C, et en ôtant la moitié de la différence de la moitié de la somme, le restant sera le plus petit angle B.
Log. de la tang. 1/2 (C - B) 8. 6946667 le nombre qui répond à cela est 5°. 16'.
4°. Les 3 côtés A B, C D, et C A, fig. 28. étant donnés, pour trouver les angles A, B, et C, du sommet de l'angle A avec l'étendue du plus petit côté A B, décrivez un cercle : alors C D sera A C et A B ; et C F sera leur différence. La règle est donc que la base B C, est la somme des côtés C D, comme la différence des côtés C F est au segment de la base C G.
Ce segment ainsi trouvé étant soustrait de la base C B, le restant est la corde G B. Ensuite du point A abaissez la perpendiculaire A E sur la corde B G, pour lors B E = E G = 1/2 G B.
Ainsi dans un triangle rectangle A E B, les côtés A B et B E étant donnés ; ou dans un triangle obliquangle A C E, les côtés A C et C E étant donnés : les angles B et A sont trouvés.
Solution des triangles rectangles sphériques par les règles communes. I. Dans un triangle rectangle sphérique deux parties quelconques étant données, outre l'angle droit, pour trouver le reste,
1°. Il faut considérer si les parties dont il est question sont conjointes ou disjointes. Si les parties disjointes sont opposées l'une à l'autre, comme si l'hypothenuse B C et l'angle C, fig. 29. sont donnés ; pour trouver le côté opposé A B, voici quelle est la règle ; le sinus total est au sinus de l'hypothénuse B C, comme le sinus de l'angle C est au sinus du côté opposé A B.
2°. Si les parties disjointes ne sont point opposées l'une à l'autre, comme si A B et l'angle adjacent B sont donnés ; pour avoir l'angle opposé C, les côtés du triangle doivent être continués du même côté, jusqu'à ce qu'ils fassent des quarts de cercle, afin que par ce moyen vous ayez un nouveau triangle, dans lequel les parties dont il est question soient opposées mutuellement les unes aux autres ; comme dans le cas présent le triangle E B F, où nous avons le côté B F donné, qui est le complément du côté A B, et l'angle B pour E F, complément de l'angle C : voici donc les règles qu'il faut suivre. Le sinus total est au sinus de B F, comme le sinus de l'angle B est au sinus E F, ou co-sinus de C.
3°. Si l'hypothénuse ne se trouve point parmi les parties conjointes, comme lorsque les côtés A B et A C sont donnés, pour avoir un angle opposé à l'un des deux ; il faut dire le sinus de A C est au sinus total, comme la tangente de A B est à la tangente de C.
4°. Mais si l'hypothénuse se trouve parmi les parties conjointes, comme si l'hypothénuse B C et l'angle C sont donnés, pour trouver le côté adjacent A C ; les côtés du triangle doivent être continués du même côté, jusqu'à ce qu'ils fassent des quarts de cercle, afin que l'on ait un nouveau triangle, dans lequel l'hypothénuse ne se trouve point parmi les parties dont il est question ; par exemple, dans le cas présent E B F dans lequel sont donnés le complément E B de l'hypothénuse B C, le complément de l'angle C, et l'angle F complément du côté A C. Puis donc que dans le triangle E F B, l'hypothénuse n'entre pas dans la question, la règle est la même que ci-dessus : c'est-à-dire, que le sinus de E F ou cosinus de C, est au sinus total, comme la tangente de E B, ou co-tangente de B C est à la tangente de F ou co-tangente de A C.
5°. Quand les côtés d'un triangle doivent être continués, il n'importe de quel côté que ce sait, pourvu qu'il ne soit pas question d'un angle aigu, autrement les côtés doivent être continués par l'autre angle oblique : si les deux côtés sont dans la connexion, ils doivent être continués par l'angle adjacent au côté en question.
C'est ainsi qu'on peut toujours former un triangle, où l'on trouve par la règle des sinus ou des tangentes les parties que l'on cherche.
Solution des triangles rectangles sphériques par une règle universelle. Considérez, comme ci-dessus, si les parties dont il est question sont conjointes ou disjointes.
Si l'un des deux côtés, qui forment l'angle droit, ou même si ces deux côtés entrent dans la question, en leur place, il faut mettre parmi les données leur complément à un quart de cercle : alors, puisque, suivant la règle universelle, si connue dans cette TRIGONOMETRIE, le sinus total avec le sinus du complément de la partie moyenne, est égal aux sinus des parties disjointes, et aux co-tangentes des parties conjointes ; ôtez du total de ces choses données, la troisième partie donnée, le reste sera quelque sinus ou tangente, et le côté ou l'angle qui y répond dans la table des logarithmes, est le côté ou l'angle que vous cherchez.
Comme la règle universelle ou générale est d'un grand secours dans la Trigonométrie, nous en ferons l'application à différents cas, et nous en apporterons des exemples qui dans les cas des parties conjointes et disjointes répandront aussi de la lumière sur la méthode commune : mais dans les cas des parties contiguès, il faudra avoir recours à d'autres solutions.
1°. L'hypothénuse B C = 60d, et l'angle C = 23d. 30'. étant donnés ; trouver le côté opposé A B, fig. 22. puisque A B est la partie moyenne, C et B C sont parties disjointes, voyez PARTIES, le sinus total, avec le co-sinus du complément A B, c'est-à-dire, avec le sinus même de A B, est égal aux sinus de C, et B C.
Le nombre qui y répond dans la table est 20d. 12'. 6'.
2°. L'hypothénuse B C = 60d. et la jambe A = 20d. 12'. 6'. étant données, trouver l'angle opposé C.
Il parait par le problème précédent que de la somme du sinus total, et du sinus du côté A B, il faut ôter le sinus de l'hypothénuse B C. le reste est le sinus de l'angle C. de sorte qu'il est aisé de transformer le cas précédent en celui-ci.
3°. Le côté A B = 20d. 12'6''& l'angle opposé C = 23d. 30'étant donnés, trouver l'hypothénuse B C.
Il parait par le premier exemple, que de la somme du sinus total, et du sinus de A B, il faut ôter le sinus de l'angle C. le reste est le sinus de l'hypothénuse B C.
4°. L'hypothénuse B C = 60d. et un côté A B = 20d. 12'16''étant donnés ; trouver l'autre côté.
Puisque B C est une partie moyenne, et que A B et A C sont des parties disjointes, le sinus total avec le co-sinus de l'hypothénuse B, sont égaux aux sinus des compléments, c'est-à-dire, aux co-sinus des côtés A B et A C.
Le nombre qui y répond dans la table, est 32d. 11'. 34''par conséquent A C est de 57d. 48'26''.
5°. Les côtés A C = 57d. 48'26''& A B = 20d. 12'6''étant donnés, trouver l'hypothénuse B C.
Il parait, par l'exemple précédent, que le sinus total doit être ôté de la somme des co-sinus des côtés A B et A C ; le reste est le co-sinus de l'hypothénuse B C. par conséquent l'exemple ci-dessus s'applique aisément à celui-ci.
6°. Le côté A C = 57d. 48'. 26''& l'angle adjacent C = 23d. 30'étant donnés, trouver l'angle opposé B.
Puisque B est une partie moyenne, et que A et C sont des parties disjointes, le sinus total avec le co-sinus de B, est égal au sinus de C, et au sinus du complément, c'est-à-dire au co-sinus de A C.
Le nombre qui y répond, dans la table est 12d. 15'. 56''. par conséquent B est de 77d. 44'. 4''.
7°. Le côté A C = 57d. 48'26''& l'angle opposé B = 77d. 44'. 4''. étant donnés, trouver l'angle adjacent C. Il parait par l'exemple précédent que le co-sinus de A C, doit être soustrait de la somme du sinus total, et du co-sinus de B, le reste est le sinus de C, de sorte que l'exemple précédent s'applique aisément à celui-ci.
8°. Les angles obliques B = 77d. 44'4''& C = 23d. 30'. étant donnés, trouver le côté A C adjacent à l'autre angle.
Il parait par le sixiéme problème que le sinus de C, doit être ôté de la somme du sinus total, et du co-sinus de B, le reste est le co-sinus de A C. Le cas du sixième problème s'applique aisément à celui-ci.
9°. Le côté A C = 57d. 48'. 26''. et l'angle adjacent C = 23d. 30'étant donnés, trouver le côté opposé A B.
Puisque A C est une partie moyenne, et que C et A B sont des parties conjointes, le sinus total, avec le sinus de A C, est égal à la co-tangente de C, et à la tangente de A B.
Le nombre qui y répond dans la table est 20d. 12'. 6''.
10°. Le côté A B = 20d. 12'6''& l'angle opposé C = 23d. 30'étant donnés, trouver le côté adjacent A C.
De la somme de la co-tangente de C et de la tangente de A B, ôtez le sinus total, le reste est le sinus de A C.
11°. Les côtés A B = 20d. 12'6''& A C = 57d. 48'26''étant donnés, trouver l'angle C, opposé à l'un des deux.
De la somme du sinus total et du sinus de A C, ôtez la tangente de B A, le reste est la co-tangente de C.
12°. L'hypothénuse B C = 60d. et l'angle oblique C = 23d. 30'. étant donnés, trouver le côté adjacent A C.
Puisque C est une partie moyenne, et que A B et A C sont des parties conjointes, le sinus total avec le co-sinus de C, sera égal à la co-tangente de A C.
Le nombre qui y répond dans les tables est 57d. 48'26''.
13°. Le côté A C = 57d. 48'26''& l'angle adjacent C = 23d. 30'étant donnés, trouver l'hypothénuse B C.
De la somme du sinus total et du co-sinus de C, ôtez la tangente de A C, le reste est la co-tangente de B C.
14°. L'hypothénuse B C = 60d. et le côté A C = 57d. 48'26''étant donnés ; trouver l'angle adjacent C.
De la somme de la co-tangente de B C, et de la tangente de A C, ôtez le sinus total, le reste est le co-sinus de C.
15°. L'hypothénuse B C = 60d. et un angle C = 23d. 30'. étant donnés, trouver l'autre angle B.
Puisque B C est la partie moyenne, et que B et e sont des parties disjointes, le sinus total avec le cosinus de B C sera égal aux co-tangentes de B et de C.
Le nombre qui y répond dans les tables est 12d. 15'56'', par conséquent B est de 77°. 44'4''.
16°. Les angles obliques B = 77d. 44'4'', et C = 23d. 30'étant donnés, trouver l'hypothénuse B C.
De la somme des co - tangentes de C et de B, soustrayez le sinus total ; le reste est le co-sinus de B C.
Solution des triangles obliquangles sphériques. 1°. Dans un triangle obliquangle sphérique A B C (Pl. Trigonom. fig. 30.) deux côtés A B et B C étant donnés conjointement avec un angle A opposé à l'un des deux ; trouver l'autre angle C. Voici la règle, le sinus du côté B C est au sinus de l'angle opposé A, comme le sinus du côté B A est au sinus de l'angle opposé C.
Le nombre qui y répond dans les tables est 82d. 34'7''.
2°. Deux angles C = 82d. 34'7''& A = 43d. 20'avec le côté A B = 60d. 45'opposé à l'un d'eux C étant donnés, trouver le côté B C opposé à l'autre angle A.
Il faut dire : le sinus de l'angle C est au sinus du côté opposé B, comme le sinus de l'angle A est au sinus du côté opposé B C. L'exemple précédent suffit pour l'intelligence de celui-ci.
3°. Deux côtés A B = 66d. 45 m. et B C = 39d. 29'avec un angle opposé à l'un des deux A = 45d. 20'étant donnés ; trouver l'angle B compris entre ces côtés ; supposez que l'angle C est aigu ; puisque l'autre angle A est pareillement aigu, la perpendiculaire B E tombe dans le triangle ; c'est pourquoi dans le triangle rectangle A B E, par le moyen de l'angle A, et du côté A B donnés, on trouve l'angle A B E. Puisque B E sert comme de partie latérale dans le triangle A E B, l'angle E B C est une partie moyenne, et le côté B C est une partie conjointe.
Ce co-sinus de l'angle E B C se trouvera en ôtant la co-tangente de A B de la somme du co - sinus de l'angle A B E, et de la co-tangente de B C. Ainsi, en joignant ensemble les angles A B E et E B C, ou si la perpendiculaire tombe hors du triangle, en ôtant l'un de l'autre, vous trouverez l'angle en question.
Le nombre qui y répond dans les tables est 20d. 25'35''par conséquent A B est de 69d. 34'25''.
Le nombre qui y répond dans les tables est 80d. 24'26''par conséquent A B C est de 79d. 9'57''.
4°. Deux angles A = 43d. 20'& B = 79d. 9'59''avec le côté adjacent A B = 66d. 45'étant donnés, trouver le côté B opposé à l'un des deux angles.
De l'un des angles donnés B, abaissez une perpendiculaire E B sur le côté inconnu A C ; &, dans le triangle rectangle A B E, par le moyen de l'angle donné A et de l'hypothénuse A B, cherchez l'angle A B E ; lequel étant ôté de l'angle A B C, il reste l'angle E B C. Mais si la perpendiculaire tombait au-dehors du triangle, en ce cas, il faudrait soustraire l'angle A B C de l'angle A B E ; parce que la perpendiculaire B E étant prise pour une des parties latérales, la partie moyenne dans le triangle A B E est l'angle B, et la partie conjointe est A B ; dans le triangle E B C, la partie moyenne est l'angle B, et la partie conjointe B C ; la co-tangente du côté B C se trouve en ôtant le cosinus de E B A de la somme de co-tangente de A B et du co-sinus de E B C. L'exemple du cas précédent s'applique aisément à celui-ci.
5°. Deux côtés A B = 66d. 45'& B C = 39d. 29'avec l'angle A opposé à l'un ou à l'autre = 43d. 20'étant donnés, trouver le troisième côté A C, abaissant, comme ci-dessus, la perpendiculaire B E, dans le triangle rectangle A B E, par le moyen de l'angle donné, et de l'hypothénuse A B, vous trouverez le côté A E ; puisqu'en prenant B E pour une partie latérale dans le triangle A E B, A B est la partie moyenne, et A E la partie disjointe, et que dans le triangle B E C, B C est la partie moyenne, et E C la partie disjointe ; le cosinus de E C se trouve en ôtant le co-sinus de A B de la somme du co-sinus de A E et C B, de sorte qu'en joignant ensemble les segments A E et E C, ou en cas que la perpendiculaire tombe hors le triangle en les ôtant l'un de l'autre, on trouvera le côté A C.
6°. Deux côtés A C = 65d. 30'46''& A B = 66d. 45'avec l'angle A = 43d. 20'compris entre ces côtés, étant donnés, trouver le troisième côté B C opposé à cet angle.
Abaissez la perpendiculaire B E, cherchez dans le triangle rectangle le segment A E, lequel étant ôté de A C, il vous reste E C. Si la perpendiculaire tombe au-dehors du triangle, il faut ôter A C de A E.
Puisqu'en prenant la perpendiculaire B E pour une partie latérale dans le triangle A E B, A B devient la partie moyenne, et A E la partie disjointe : et que dans le triangle E B C, C B est la partie moyenne, et E C la partie disjointe ; le co-sinus de B C se trouve en ôtant le co-sinus de A E, de la somme des co-sinus de A B et E C.
7°. Deux angles A = 43d. 20'& B = 79d. 9'59''avec le côté C B = 39d. 29'opposé à l'un ou l'autre de ces angles, étant donnés, trouver le côté A B adjacent à l'un et l'autre.
Abaissez la perpendiculaire C D de l'angle inconnu C sur le côté opposé A B, et si cette perpendiculaire tombe dans le triangle, par le moyen de l'angle donné B, et de l'hypothénuse B C, cherchez dans le triangle rectangle B C D, le segment B D. Puisqu'en prenant la perpendiculaire C D pour une partie latérale dans le triangle C D B, D B est la partie moyenne, et l'angle B une partie conjointe ; et que dans le triangle C D A, A D est la partie moyenne, et l'angle A une partie conjointe ; le sinus du segment A D se trouve en ôtant la co-tangente de l'angle B de la somme du sinus de D B et de la co-tangente de l'angle A ; de sorte qu'en joignant ensemble les segments A D et D B, ou, si la perpendiculaire tombe hors du triangle, en ôtant l'un de l'autre, le résultat sera du côté A B que vous cherchiez.
8°. Deux côtés A B = 66d. 45'. et B C = 39d. 29'. avec l'angle compris entre ces côtés = 79d. 9'. 59''. étant donnés, trouver l'angle A opposé à l'un ou à l'autre de ces côtés.
En abaissant la perpendiculaire C D, vous trouverez le segment B D, comme dans le problème précédent : ôtez ce segment de A B, reste A D. Si la perpendiculaire tombe hors le triangle, A B doit être joint à D B : et comme en prenant la perpendiculaire C D pour une partie latérale dans le triangle C D B, B D est la partie moyenne, et l'angle B la partie conjointe ; et que dans le triangle C D A, A D est la partie moyenne, et l'angle A la partie conjointe ; la co-tangente de l'angle A se trouve en ôtant le sinus de D B de la somme de la co-tangente de l'angle B et du sinus A D.
9°. Deux angles A = 43d. 20'. et B = 79d. 9'. 59''. avec le côté adjacent A B = 76d. 45'. étant donnés, trouver l'angle C opposé à ce côté.
De l'un des angles donnés B abaisser la perpendiculaire B E, sur le côté opposé A C : dans le triangle rectangle A B E, par le moyen de l'angle A donné, et de l'hypothénuse A B, vous trouverez l'angle A B E, lequel étant ôté de A B C, reste l'angle E B C.
Si la perpendiculaire tombe hors le triangle, il faut ôter A B C de A B E. Puisqu'en prenant B E pour une partie latérale dans le triangle C E B, l'angle C est la partie moyenne, et l'angle C B E, la partie disjointe ; et que dans le triangle A B E, l'angle A est la partie moyenne et l'angle A B E la partie disjointe : le co-sinus de l'angle C se trouve en soustrayant le sinus de l'angle A B E de la somme du cosinus de l'angle A et du sinus de E B C.
10°. Deux angles A = 42d. 20'& C = 82d. 34'. avec le côté B A = 66d. 45'opposé à l'un de ces deux, étant donnés, trouver l'autre angle.
De l'angle cherché B, abaissez une perpendiculaire B E, et dans le triangle rectangle A E B, par le moyen de l'angle donné A, et de l'hypothénuse B A, vous trouverez l'angle A B E, puisqu'en prenant la perpendiculaire E B pour une partie latérale dans le triangle E B C, l'angle C est la partie moyenne, et l'angle C E B la partie disjointe ; et que dans le triangle A B E, l'angle A est la partie moyenne, et l'angle A B E la partie disjointe : le sinus de l'angle E B C se trouve en soustrayant le co-sinus de A de la somme du co-sinus de C et du sinus de A B E, de-sorte qu'en joignant ensemble A B E et E B C ; ou si la perpendiculaire hors le triangle, en ôtant l'un de l'autre vous aurez pour résultat l'angle cherché A B C.
11°. Les trois côtés étant donnés, trouver un angle opposé à l'un de ces côtés.
I. Si un côté A C, fig. 16. est un quart de cercle, et que le côté A B soit plus petit qu'un quart de cercle, vous trouverez l'angle A ; prolongez A B jusqu'en F, et jusqu'à ce que A F soit égal à un demi-cercle ; du pôle A tirez l'arc C F, qui coupe l'arc B F à angles droits en F. Puisque dans le triangle rectangle C B F, l'hypothénuse B C est donnée, et le côté F B, ou son complément A B, à un demi-cercle, vous trouverez la perpendiculaire C F, laquelle étant la mesure de l'angle C A B, donne par conséquent l'angle que vous cherchez.
II. Si l'un des côtés A C est un quart de cercle, et que l'autre côté A B soit plus grand qu'un quart de cercle, cherchez l'angle A : de A B ôtez le quart de cercle A D ; et du pôle A décrivez l'arc C D, coupant l'arc A B à angles droits en D. Comme dans le triangle rectangle C D B, l'hypothénuse B C, et le côté D B, ou l'excès du côté A B sur le quart de cercle sont donnés, la perpendiculaire C D sera trouvée, comme ci-dessus, et cette perpendiculaire est la mesure de l'angle cherché A.
III. Si le triangle est isoscele, que B C = C F et l'angle A C F celui qu'on cherche ; coupez A F en deux parties égales au point D ; et par D et C faites passer l'arc de cercle D C. Puisque D C est perpendiculaire à A F, les angles A et F, A C D et D C F sont égaux ; par le moyen de l'hypothénuse A C et du côté A D donnés dans le triangle rectangle A C D, vous trouverez l'angle A C D, dont le double est l'angle cherché A C F ; et par les mêmes parties données on peut trouver l'angle A ou l'angle F.
IV. Si le triangle est scalène, et que vous cherchiez l'angle A, fig. 30. de C, abaissez la perpendiculaire C D, et cherchez la demi-différence des segments A D et D B, en disant, la tangente de la moitié de la base A B est à la tangente de la moitié de la somme des côtés A C et C B, comme la tangente de leur demi-différence est à la tangente de la demi-différence des segments A D et D B : ajoutez ensuite la demi-différence des segments à la moitié de la base pour trouver le grand segment, et ôtez cette même demi-différence de la même moitié de la base pour trouver le petit segment, pour lors ayant trouvé dans le triangle rectangle C A D, l'hypothénuse A C et le côté A D, vous avez aussi l'angle cherché A. De la même manière, dans l'autre triangle C D B, vous trouverez B par les parties données C B et D B.
12°. Les trois angles A, B et C étant donnés, trouver un des côtés quelconque.
Comme, au-lieu du triangle donné on peut en prendre un autre, dont les côtés soient égaux aux angles donnés, et les angles égaux aux côtés donnés, ce problème se résout de la même manière que le précédent. Chambers et Wolf. (E)
TRIANGLE, s. m. en Astronomie, c'est un nom commun à deux constellations, l'une dans l'hémisphère septentrional, appelé simplement triangle ou triangle céleste, et l'autre dans l'hémisphère méridional, que l'on appelle triangle austral. Voyez CONSTELLATION.
Les étoiles qui composent le triangle septentrional, sont au nombre de quatre, suivant le catalogue de Ptolémée, autant dans celui de Tycho ; 24 dans le catalogue britannique.
TRIANGLE différentiel d'une courbe, dans la haute Géométrie, c'est un triangle rectiligne rectangle, dont l'hypothénuse est une partie de la courbe, qui ne diffère qu'infiniment peu d'une ligne droite. Voyez COURBE.
Supposons, par exemple, la demi-ordonnée p m, Pl. d'analyse, fig. 18. et une autre demi-ordonnée P M, qui en soit infiniment proche ; alors P p sera la différentielle de l'abscisse, et abaissant une perpendiculaire M R = P p, R m sera la différentielle de la demi-ordonnée. Tirez donc une tangente T M, et l'arc infiniment petit M m ne sera pas différent d'une ligne droite ; par conséquent M m R est un triangle rectiligne rectangle, et constitue le triangle différentiel de cette courbe. Voyez TANGENTE et SOUTANGENTE. Chambers. (O)
TRIANGLE, (Arithmétique) on appelle ainsi un triangle formé de la manière suivante.
La première colonne verticale renferme l'unité ; la seconde la suite des nombres naturels 2, 3, 4, 5, etc. la troisième la suite des nombres triangulaires, 1, 3, 6, 10, etc. la quatrième la suite des nombres pyramidaux, etc. Sur quoi voyez l'article FIGURE ; voyez aussi TRIANGULAIRE, PYRAMIDAL, etc. M. Pascal a fait un traité de ce triangle arithmétique. Les bandes horizontales sont les coefficiens des différentes puissances du binome. Sur quoi voyez BINOME. (O)
TRIANGLE, (Littérature) cette figure géométrique a depuis longtemps servi de signe, de marque, ou de symbole à bien des choses différentes. Plutarque nous apprend que le philosophe Xénocrates comparait la divinité à un triangle équilatéral, les génies au triangle isoscele, et les hommes au scalene. Les Chrétiens à leur tour employèrent le triangle pour représenter la Trinité ; d'abord ils se servirent du simple triangle, mais dans la suite ils ajoutèrent au triangle quelques lignes, qui formaient une croix : c'est ainsi qu'on trouve des triangles diversement combinés sur les médailles des papes publiées par Bonanni. Au commencement de la découverte de l'Imprimerie, rien n'était plus commun que de graver ces sortes de figures au frontispice des livres ; ensuite elles devinrent de simples marques de correcteur d'Imprimerie, ou des symboles distinctifs dans le commerce. Enfin, elles ont passé aux emballeurs, qui marquent ainsi avec leur pinceau, toutes les balles de marchandises qui sont envoyées dans les provinces, ou qui doivent passer à l'étranger. (D.J.)
TRIANGLE, (Fortification) ouvrage dont les trois angles sont formés par des bastions coupés, ou des demi - bastions. (D.J.)
TRIANGLE, (Marine) sorte d'échafaud, qui sert à travailler sur les côtés du vaisseau. Il est composé de trois pièces ; d'un traversin ; d'une accore, qui pend de travers sur le traversin, et qui Ve s'appuyer sur le côté du vaisseau ; et d'un arcboutant, qui est attaché par une extrémité au bout du traversin, et qui, s'élevant par l'autre en-haut du vaisseau, est cloué à son côté.
TRIANGLE, (Marine) c'est le nom qu'on donne à trois barres de cabestan, qu'on suspend autour des grands mâts, quand on veut le racler.
TRIANGLE, (Instrument d'Ouvrier) les Menuisiers, les Charpentiers, et quelques autres ouvriers, ont des instruments à qui ils donnent le nom de triangle, et les spécifient néanmoins par quelque terme qui dénote leur usage. Le triangle onglé ou à onglet, n'est qu'une règle de bois de deux lignes d'épais, d'un pied de long, et de trois pieds de large, dont l'une des extrémités, qui est coupée en angle de quarante-cinq degrés, est emboitée dans un autre morceau de bois plus épais, qu'on nomme la joue. Il sert à tracer des angles réguliers, en appuyant la pièce de bois contre la joue de l'instrument, et en tirant une ligne le long de la règle. Le triangle carré est une vraie équerre, dont une des branches qu'on appelle la joue, qui est du triple plus épaisse que l'autre, a dans le milieu et tout le long de son épaisseur, une espèce de languette. Il sert à tracer les pièces carrées, en les appuyant sur la languette le long de la joue, et en tirant les lignes parallèles à l'autre branche. Pour éviter la multiplicité des instruments, le sieur Hulin en a inventé un qui contient non-seulement ces deux triangles, mais encore une équerre, et ce qu'on appelle la pièce carrée ; mais les Anglais ont imaginé un autre instrument encore plus simple et plus parfait.
Articles populaires Science
ROTATION
S. f. terme en usage dans la Mécanique, pour exprimer le mouvement d'un corps qui roule ou qui tourne. Voyez ROUE, etc.ROTATION, en terme de Géométrie, signifie la révolution d'une surface autour d'une ligne immobile, qu'on appelle l'axe de rotation. Voyez AXE.
Les surfaces planes engendrent ou forment des solides par leur rotation. Voyez SOLIDE et ENGENDRER.
Lire la suite...