S. f. en Géométrie, c'est une ligne qui traverse un parallelogramme, ou toute autre figure quadrilatère, et qui Ve du sommet d'un angle au sommet de celui qui lui est opposé.
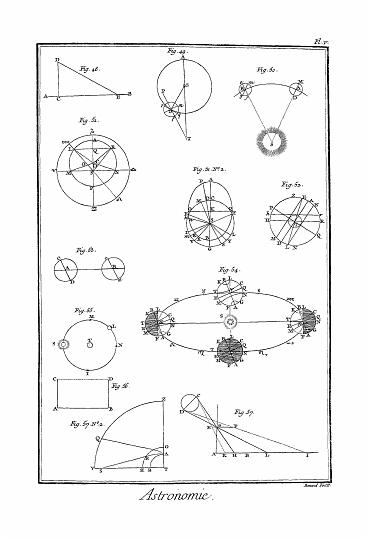
Telle est la ligne P N (Pl. géomét. fig. 24.) tirée de l'angle P à l'angle N. Voyez FIGURE. Quelques auteurs l'appellent diamètre, d'autres le diamétral de la figure ; mais ces noms ne sont point d'usage.
Il est démontré 1°. que toute diagonale divise un parallélogramme en deux parties égales : 2°. que deux diagonales tirées dans un parallélogramme se coupent l'une l'autre en deux parties égales : 3°. que la diagonale d'un carré est incommensurable avec l'un des côtés. Voyez PARALLELOGRAMME, QUARRE, etc.
La somme des carrés des deux diagonales de tout parallélogramme, est égale à la somme des carrés des quatre côtés.
Il est évident que la fameuse quarante-septième proposition d'Euclide (Voyez HYPOTHENUSE), n'est qu'un cas particulier de cette proposition : car si le parallélogramme est rectangle, on voit tout de suite que les deux diagonales sont égales, et par conséquent que le carré d'une diagonale, ou ce qui est la même chose, que le carré de l'hypothenuse d'un angle droit est égal à la somme des carrés des deux côtés. Si un parallélogramme est obliquangle, et qu'ainsi ses deux diagonales soient inégales, comme il arrive le plus souvent, la préposition devient d'un usage beaucoup plus étendu.
Voici la démonstration par rapport au parallélogramme obliquangle. Supposons le parallélogramme obliquangle A B C D (Pl. géom. fig. 25.), dont B D est la plus grande diagonale, et A C la plus petite : du point A de l'angle obtus D A B, abbaissez une perpendiculaire A E sur le côté C D ; et du point B, une autre perpendiculaire B F sur le côté D C : alors les triangles A D E, B C F, sont égaux et semblables, puisque A D est égal à B C, et que les angles A D E, B C F, aussi bien que A E D, B F C, sont aussi égaux ; par conséquent D E est égal à C F. Maintenant (par la 12e. proposition d'Euclide, liv. II.) dans le triangle B D C obtus-angle, le carré du côté B D est égal à la somme des carrés de B C et C D, et en outre, au double du rectangle de C F par C D ; et par la treizième du livre II. dans le triangle D A C, le carré du côté A C est égal à la somme des carrés de A D et C D, en ôtant le double du rectangle du même côté C D par D E = C F : ainsi ce défaut étant précisément compensé par le premier excès, la somme des carrés des deux diagonales est égale à la somme des carrés des quatre côtés, G Q F D.
Remarquez que cette démonstration suppose la fameuse quarante-septième proposition d'Euclide, et qu'ainsi pour en déduire cette proposition, il faut se passer de cette quarante-septième : autrement on donnerait dans un cercle vicieux. Ceux donc qui prétendraient, en conséquence de la démonstration ci-dessus, que la quarante-septième n'est qu'un corollaire de celle-ci, se tromperaient ; elle en est un cas, mais non un corollaire.
Ainsi dans tout rhombe ou losange connaissant un côté et une diagonale, on connaitra pareillement l'autre diagonale : car comme les quatre côtés sont égaux, en ôtant le carré de la diagonale donnée du quadruple du carré du côté donné, le reste est le carré de la diagonale cherchée.
Cette proposition est aussi d'un grand usage dans la théorie des mouvements composés : car dans un parallélogramme obliquangle, la plus grande diagonale étant la soutendante d'un angle obtus, et la plus petite d'un angle aigu ; qui est le complément du premier ; la plus grande diagonale sera d'autant plus grande, et la plus petite sera d'autant plus petite, que l'angle obtus sera plus grand : de sorte que si l'on conçoit que l'angle obtus croisse jusqu'à devenir infiniment grand par rapport à l'angle aigu, ou ce qui revient au même, si les deux côtés contigus du parallélogramme sont étendus directement bout à bout en ligne droite, la grande diagonale devient la somme des deux côtés, et la plus petite s'anéantit. Maintenant deux côtés contigus d'un parallélogramme étant connus avec l'angle qu'ils renferment, il est aisé de trouver en nombre la soutendante de cet angle, c'est-à-dire une des diagonales du parallélogramme : quand cela est fait, la proposition donne l'autre. La seconde diagonale ainsi trouvée, est la ligne que décrirait un corps poussé en même temps par deux forces, qui auraient entr'elles le même rapport que les côtés contigus, qui désignent les directions suivant lesquelles ces forces agissent : le corps décrirait cette diagonale en même temps qu'il parcourait l'un ou l'autre des deux côtés contigus, s'il n'était poussé que par la force qui correspond à chaque côté : c'est-là un des grands usages de cette proposition ; car le rapport de deux forces, et l'angle qu'elles font, étant donnés, on a besoin quelquefois de déterminer en nombres la ligne qu'un corps poussé par ces deux forces décrirait dans un certain temps. Voyez COMPOSITION et MOUVEMENT.
Les côtés d'une figure rectiligne, comme A B, A E, C D, D E (figure 26.), excepté B C ; et les angles A, E, D, o, y, excepté B, C, étant donnés, trouver les diagonales.
Dans le triangle A B E, les côtés A B et A E étant donnés, l'angle E se trouve aisément par la Trigonométrie, et ensuite la diagonale B E : on résout de la même manière le triangle B C D, et l'on détermine la diagonale B D.
Comme les ichnographies ou les plans se font plus commodément lorsque l'on a les côtés et les diagonales, l'usage de ce problème est de quelque importance en planimétrie, particulièrement à ceux qui veulent faire un ouvrage exact, quoiqu'il leur en coute du calcul. Voyez ICHNOGRAPHIE, etc. (E)
Articles populaires Science
PERFECTION
S. f. (Métaphysique) c'est l'accord qui règne dans la variété de plusieurs choses différentes, qui concourent toutes au même but. Tout composé fait dans de certaines vues est plus ou moins parfait, à proportion que ses parties s'assortissent exactement à ces vues. L'oeil, par exemple est un organe de plusieurs pièces qui doivent toutes servir à tracer une image claire et distincte de l'objet visible au fond de la rétine. Si toutes ces pièces servent autant qu'elles en sont capables, à cet usage, l'oeil est censé parfait. La vie de l'homme, entant qu'elle désigne l'assemblage de ses actions libres, est censée parfaite, si toutes ses actions tendent à une fin qui leur soit commune avec les actions naturelles. Car de-là résulte cet accord entre les actions naturelles et les actions libres, dans lequel consiste la perfection de la vie humaine. Au contraire l'imperfection, ou le mal métaphysique, consiste dans la contrariété de diverses choses qui s'écartent d'un même but.Lire la suite...