S. m. (Métaphysique) système n'est autre chose que la disposition des différentes parties d'un art ou d'une science dans un état où elles se soutiennent toutes mutuellement, et où les dernières s'expliquent par les premières. Celles qui rendent raison des autres s'appellent principes, et le système est d'autant plus parfait, que les principes sont en plus petit nombre : il est même à souhaiter qu'on les réduise à un seul. Car de même que dans une horloge il y a un principal ressort duquel tous les autres dépendent, il y a aussi dans tous les systèmes un premier principe auquel sont subordonnées les différentes parties qui le composent.
On peut remarquer dans les ouvrages des philosophes trois sortes de principes, d'où se forment trois sortes de systèmes. Les uns sont des maximes générales ou abstraites. On exige qu'ils soient si évidents ou si bien démontrés, qu'on ne les puisse révoquer en doute. La vertu que les philosophes leur attribuent est si grande, qu'il était naturel qu'on travaillât à les multiplier. Les métaphysiciens se sont en cela distingués. Descartes, Malebranche, Leibnitz, etc. chacun à l'envi nous en a prodigués ; et nous ne devons plus nous en prendre qu'à nous-mêmes, si nous ne pénétrons pas les choses les plus cachées. Les principes de la seconde espèce sont des suppositions qu'on imagine pour expliquer les choses dont on ne saurait d'ailleurs rendre raison. Si les suppositions ne paraissent pas impossibles, et si elles fournissent quelque explication des phénomènes connus, les philosophes ne doutent pas qu'ils n'aient découvert les vrais ressorts de la nature. Une supposition qui donne des dénouements heureux, ne leur parait pas pouvoir être fausse. De-là cette opinion que l'explication des phénomènes prouve la vérité d'une supposition, et qu'on ne doit pas tant juger d'un système par ses principes, que par la manière dont il rend raison des choses. C'est l'insuffisance des maximes abstraites qui a obligé d'avoir recours à ces sortes de suppositions. Les métaphysiciens ont été aussi inventifs dans cette seconde espèce de principes que dans la première. Les troisiemes principes sont des faits que l'expérience a recueillis, qu'elle a consultés et constatés. C'est sur les principes de cette dernière espèce que sont fondés les vrais systèmes, ceux qui mériteraient seuls d'en porter le nom. Conséquemment à cela, j'appellerai systèmes abstraits ceux qui ne portent que sur des systèmes abstraits ; hypothèses, ceux qui n'ont que des suppositions pour fondement ; et vrais systèmes, ceux qui ne s'appuyent que sur des faits bien prouvés.
M. l'abbé de Condillac, dans son traité des systèmes, s'est appliqué surtout à décrire tous les systèmes abstraits. Selon lui, il y a trois sortes de principes abstraits en usage. Les premiers sont des propositions générales exactement vraies dans tous les cas. Les seconds sont des propositions vraies par les côtés les plus frappans ; et que pour cela on est porté à supposer vraies à tous égards. Les derniers sont des rapports vagues qu'on imagine entre des choses de différente nature. Les premiers ne conduisent à rien. Qu'un géomètre, par exemple, médite tant qu'il voudra ces maximes, le tout est égal à toutes ses parties ; à des grandeurs égales, ajoutez des grandeurs égales, les tous seront égaux ; ajoutez-en d'inégales, ils seront inégaux : aura-t-il là de quoi devenir un profond géomètre ? S'il n'est donné à aucun homme de devenir, après quelques heures de méditation, un Condé, un Turenne, un Richelieu, un Colbert ; quoique l'art militaire, la politique et les finances aient comme toutes les autres sciences leurs principes généraux, dont on peut en peu de temps découvrir toutes les conséquences : pourquoi un philosophe deviendrait-il tout-à-coup un homme savant, un homme pour qui la nature n'a point de secrets ; et cela par le charme de deux ou trois propositions ? Ce seul parallèle suffit pour faire voir combien s'abusent ces philosophes spéculatifs, qui aperçoivent une si grande fécondité dans les principes généraux. Les deux autres ne mènent qu'à des erreurs. Et c'est ce que l'auteur du traité des systèmes prétend prouver, par les différents systèmes qu'il parcourt. Bayle, Descartes, Malebranche, Leibnitz, l'auteur de l'action de Dieu sur la créature, et Spinosa, lui fournissent des exemples de ce qu'il avance. En général le grand défaut des systèmes abstraits, c'est de rouler sur des notions vagues et mal déterminées, sur des mots vides de sens, sur des équivoques perpétuelles. M. Locke compare ingénieusement ces faiseurs de systèmes à des hommes, qui sans argent et sans connaissance des espèces courantes, compteraient de grosses sommes avec des jetons, qu'ils appelleraient louis, livre, écu. Quelques calculs qu'ils fissent, leurs sommes ne seraient jamais que des jetons : quelques raisonnements que fassent des philosophes à systèmes abstraits, leurs conclusions ne seront jamais que des mots. Or de tels systèmes, loin de dissiper le chaos de la métaphysique, ne sont propres qu'à éblouir l'imagination par la hardiesse des conséquences où ils conduisent, qu'à séduire l'esprit par des fausses lueurs d'évidence, qu'à nourrir l'entêtement par les erreurs les plus monstrueuses, qu'à éterniser les disputes, ainsi que l'aigreur et l'emportement avec lequel on les soutient. Ce n'est pas qu'il n'y ait de ces systèmes qui ne méritent les éloges qu'on leur donne. Il y a tels de ces ouvrages qui nous forcent à les admirer. Ils ressemblent à ces palais où le gout, les commodités, la grandeur, la magnificence concouraient à faire un chef-d'œuvre de l'art ; mais qui ne porteraient que sur des fondements si peu solides, qu'ils paraitraient ne se soutenir que par enchantement. On donnerait sans-doute des éloges à l'architecte ; mais des éloges bien contrebalancés par la critique qu'on ferait de son imprudence. On regarderait comme la plus insigne folie d'avoir bâti sur de si faibles fondements un si superbe édifice ; et quoique ce fût l'ouvrage d'un esprit supérieur, et que les pièces en fussent disposées dans un ordre admirable, personne ne serait assez peu sage pour y vouloir loger.
Par la seule idée qu'on doit se faire d'un système, il est évident qu'on ne peut qu'improprement appeler système ces ouvrages, où l'on prétend expliquer la nature par le moyen de quelques principes abstraits. Les hypothèses, quand elles sont faites suivant les règles que nous en avons données, méritent mieux le nom de système. Nous en avons fait voir les avantages. Voyez l'article HYPOTHESE.
Les vrais systèmes sont ceux qui sont fondés sur des faits. Mais ces systèmes exigent un assez grand nombre d'observations, pour qu'on puisse saisir l'enchainement des phénomènes. Il y a cette différence entre les hypothèses et les faits qui surviennent des principes, qu'une hypothèse devient plus incertaine à mesure qu'on découvre un plus grand nombre d'effets, dont elle ne rend pas raison : au-lieu qu'un fait est toujours également certain, et il ne peut cesser d'être le principe des phénomènes, dont il a une fois rendu raison. S'il y a des effets qu'il n'explique pas, on ne doit pas le rejeter, on doit travailler à découvrir les phénomènes qui le lient avec eux, et qui forment de tous un seul système.
Il n'y a point de science ni d'art où l'on ne puisse faire des systèmes : mais dans les uns, on se propose de rendre raison des effets ; dans les autres, de les préparer et de les faire naître. Le premier objet est celui de la physique ; le second est celui de la politique. Il y a des sciences qui ont l'un et l'autre, telles sont la Chimie et la Médecine.
SYSTEME, s. m. (Philosophie) signifie en général un assemblage ou un enchainement de principes et de conclusions : ou bien encore, le tout et l'ensemble d'une théorie dont les différentes parties sont liées entr'elles, se suivent et dépendent les unes des autres.
Ce mot est formé d'un mot grec qui signifie composition ou assemblage.
C'est dans ce sens-là que l'on dit un système de Philosophie, un système d'Astronomie, etc. le système de Descartes, celui de Newton, etc. Les Théologiens ont formé une quantité de systèmes sur la grâce.
Gassendi a renouvellé l'ancien système des atomes, qui était celui de Démocrite, suivi par Epicure, Lucrèce, etc. Voyez CORPUSCULAIRE, ATOME et MATIERE.
Les expériences et les observations sont les matériaux des systèmes. Aussi rien n'est-il plus dangereux en Physique, et plus capable de conduire à l'erreur, que de se hâter de faire des systèmes, sans avoir auparavant le nombre de matériaux nécessaires pour les construire. Ce n'est souvent qu'après un très-grand nombre d'expériences qu'on parvient à entrevoir la cause d'un effet, et il y en a même plusieurs, sur lesquelles des expériences répétées et variées à l'infini, n'ont pu encore nous éclairer. Le Cartésianisme qui avait succédé au Péripatétisme, avait mis le goût des systèmes fort à la mode. Aujourd'hui, grâce à Newton, il parait qu'on est revenu de ce préjugé, et qu'on ne reconnait de vraie physique que celle qui s'appuie sur les expériences, et qui les éclaire par des raisonnements exacts et précis, et non pas par des explications vagues. Voyez EXPERIENCE et EXPERIMENTAL.
SYSTEME, en terme d'Astronomie, est la supposition d'un certain arrangement des différentes parties qui composent l'univers ; d'après laquelle hypothèse les Astronomes expliquent tous les phénomènes ou apparences des corps célestes, etc. Voyez ASTRONOMIE, PLANETE, etc.
Il y a dans l'Astronomie trois systèmes principaux, sur lesquels les philosophes ont été partagés : le système de Ptolémée, celui de Copernic, et celui de Tycho-Brahé.
Le système de Ptolémée place la terre immobîle au centre de l'univers, et fait tourner les cieux autour de la Terre d'orient en occident ; de sorte que tous les corps célestes, astres et planètes suivent ce mouvement. Voyez PTOLEMEE.
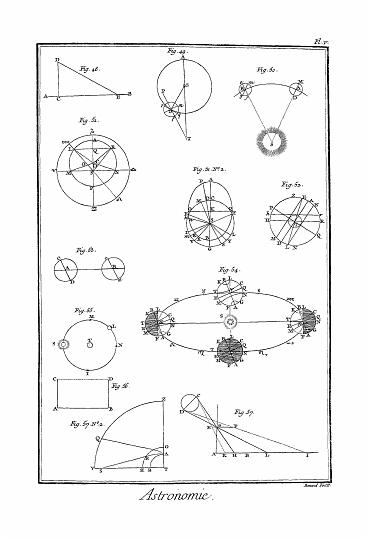
Pour ce qui est de l'ordre et des distances des différents corps qui entrent dans ce système, les voici. D'abord la Lune tourne autour de la Terre ; ensuite Vénus, puis Mercure, le Soleil, Mars, Jupiter et Saturne. Tous ces astres, selon Ptolémée, tournaient autour de la Terre en vingt-quatre heures ; et ils avaient outre cela un mouvement particulier par lequel ils achevaient leurs révolutions annuelles. Voyez Pl. astron. fig. xliij.
Les principaux partisans de ce système sont Aristote, Hipparque, Ptolémée et un grand nombre d'anciens philosophes que tout l'univers a suivis pendant plusieurs siècles, et que suivent encore plusieurs universités et autres collèges d'où l'on a banni la liberté de philosopher ; mais les observations des derniers temps ont entièrement détruit ce système ; et même aujourd'hui on ne manque pas de démonstrations pour l'anéantir absolument. Voyez TERRE, etc.
En effet, les observations nous apprennent qu'en quelque lieu que l'on place le Soleil, il faut nécessairement reconnaître qu'il est renfermé dans l'orbite de Vénus, puisque cette planète parait passer tantôt derrière le Soleil, tantôt entre le Soleil et la terre. Donc l'orbite du Soleil ne saurait entourer celle de Vénus, comme elle l'entoure dans le système de Ptolémée. Il en est de même de Mercure qui est presque perpétuellement plongé dans les rayons du Soleil, et qui, parce qu'il s'en écarte beaucoup moins que Vénus, doit par cette raison avoir une orbite beaucoup plus petite.
D'ailleurs, nous n'exposons ici que ce qu'il y a de plus simple dans le système de Ptolémée. Si nous y ajoutions tous les cieux de crystal qu'il imaginait pour rendre raison des différents phénomènes célestes, c'en serait assez à un bon esprit pour rejeter entièrement cette hypothèse.
Le système de Copernic place le Soleil immobîle au centre de l'univers, si ce n'est qu'il donne au Soleil un mouvement de rotation autour de son axe. Voyez SOLEIL.
Autour de lui tournent d'occident en orient, et dans différentes orbites, Mercure, Vénus, la Terre, Mars, Jupiter et Saturne. Voyez PLANETE.
La Lune tourne dans une orbite particulière autour de la Terre, et elle l'accompagne dans tout le cercle qu'elle décrit autour du Soleil. Voyez LUNE.
Quatre satellites tournent de même autour de Jupiter, et cinq autour de Saturne. Voyez SATELLITE.
Dans la région des planètes sont les cometes qui tournent autour du Soleil, mais sur des orbites fort excentriques, le Soleil étant placé dans un de leurs foyers. Voyez COMETE.
A une distance immense, au-delà de la région des planètes et des cometes, sont les étoiles fixes. Voyez ÉTOILE.
Les étoiles, eu égard à l'immensité de leur distance, et au peu de rapport qu'elles paraissent avoir à notre monde, ne sont pas censées en faire partie. Il est très-probable que chaque étoîle est elle-même un soleil et le centre de l'univers et de son immensité, et toutes les observations s'accordent à en prouver la vérité. Voyez COPERNIC.
Le système qu'on vient d'exposer, est le plus ancien ; c'est le premier qui ait été introduit par Pythagore en Grèce et en Italie, où il a été appelé pendant plusieurs siècles le système pythagoricien : il fut suivi par Philolaus, Platon, Archimède, etc. Il se perdit sous le règne de la philosophie péripatéticienne ; mais enfin il fut remis en vigueur heureusement il y a plus de deux cent ans, par Nicolas Copernic dont il porte aujourd'hui le nom. Voyez-en le plan, Pl. astron. fig. xliv. Voyez aussi COPERNIC.
Le système de Tycho-Brahé revient, à plusieurs égards, à celui de Copernic ; mais dans celui de Tycho-Brahé l'on suppose la terre immobile, on supprime son orbite que l'on remplace par l'orbite du Soleil qui tourne autour de la terre, tandis que toutes les autres planètes, excepté la Lune et les satellites, tournent autour de lui.
Mais il n'y a aucune raison ni aucun phénomène dans la nature qui oblige d'avoir recours à un subterfuge si manifeste, que l'auteur n'a employé lui-même que par le motif de la persuasion superstitieuse où il était que c'était une chose contraire à l'Ecriture, que de supposer le Soleil immobîle et la Terre en mouvement : ce scrupule n'a pas donné un échec bien considérable au vrai système.
L'Ecriture, dans les endroits où elle semble supposer le mouvement de la Terre, parle conformément aux idées vulgairement reçues, et aux simples apparences. C'est pourquoi on ne saurait taxer d'hérésie ceux qui soutiennent l'opinion contraire, une telle matière n'intéressant ni les mœurs ni la foi. D'ailleurs, la loi découverte par Kepler dans les mouvements des planètes, et expliquée si heureusement par le célèbre Newton, fournit une démonstration directe contre le système de Ticho-Brahé.
Kepler a observé, que les temps des révolutions des planètes autour du Soleil, avaient un certain rapport avec leurs distances à cet astre, et on a trouvé que la même loi s'observait dans les satellites de Jupiter et de Saturne ; et M. Newton a fait voir que cette loi si admirable était une suite nécessaire de la gravitation de toutes les planètes vers le Soleil, et de la gravitation des satellites vers leurs planètes principales, en raison inverse du carré des distances. Desorte que si la Lune et le Soleil tournaient autour de la terre, il faudrait que ces deux planètes gravitassent ou pesassent vers la terre, comme font les autres planètes vers le Soleil, et que les temps des révolutions du Soleil et de la Lune autour de la Terre fussent entr'eux dans le rapport que la loi de Kepler établit ; c'est-à-dire, comme les racines carrées des cubes de leurs distances à la Terre. Or ces temps ne sont point du-tout dans ce rapport ; d'où il s'ensuit que le Soleil et la Lune ne tournent point autour de la Terre comme centre commun. Voyez le plan du système de Tycho, fig. xlv. astron.
On se sert aussi en général du mot de système pour marquer une certaine disposition ou arrangement que plusieurs corps ont les uns par rapport aux autres. Ainsi dans la mécanique, l'assemblage de plusieurs corps qui se meuvent ou qui sont en repos, sur un plan ou sur une surface quelconque, s'appelle un système de corps ; une verge chargée de trois corps, est un système de trois corps, etc. Chambers. (O)
SYSTEME, en Anatomie, c'est un assemblage des parties d'un tout ; c'est dans ce sens qu'en parlant de tous les vaisseaux sanguins, on dit le système des vaisseaux sanguins, de tous les nerfs, le système des nerfs, &c.
SYSTEME, (Belles Lettres) en poésie, se dit d'une hypothèse que le poète choisit, et dont il ne doit jamais s'éloigner.
Par exemple, s'il fait son plan selon la Mythologie, il doit suivre le système fabuleux, s'y renfermer dans tout le cours de son ouvrage, sans y mêler aucune idée de Christianisme : si au contraire il traite un sujet chrétien, il doit en écarter toute hypothèse de paganisme. Voyez INVOCATION, MUSES, etc.
Ainsi dès qu'une fois il a invoqué Apollon, il doit s'abstenir de mettre sur la scène le vrai Dieu, les anges ou les saints, afin de ne point confondre les deux systèmes. Il est vrai que le système fabuleux est plus gai, plus riche, plus figuré ; mais d'un autre côté quelle figure font, et quel rôle peuvent jouer dans un poème chrétien les dieux du paganisme ? Le père Bouhours observe que le système de la poésie est de sa nature entièrement payen et fabuleux, et plusieurs auteurs l'ont pensé comme lui ; mais cette opinion n'est pas universelle, et d'autres écrivains célèbres ont prouvé que les fictions de la Mythologie ne sont nullement essentielles à la poésie ; qu'aujourd'hui même elles ne sont plus de saison, et qu'un poème pour plaire et pour intéresser n'a pas besoin de tout cet attirail de divinités et de machines qu'employaient les anciens. Voyez MACHINE et MERVEILLEUX.
SYSTEME, dans l'Art militaire, est l'arrangement d'une armée, ou la disposition de toutes les parties de la fortification, suivant les idées particulières d'un général ou d'un ingénieur.
Ainsi l'on dirait qu'un ordre de bataille ou un ordre d'attaquer est, suivant le système de M. de Folard, s'il était conforme à l'arrangement prescrit par cet auteur ; et de même qu'une ville est fortifiée selon le système de M. de Vauban, lorsque sa fortification est disposée selon les règles de ce fameux ingénieur. Voyez à la suite du mot FORTIFICATION, les principaux systèmes de fortification.
Bien des gens se plaignent de notre fortification actuelle, qu'ils jugent mauvaise par le peu de résistance des places. On souhaiterait d'avoir une méthode plus parfaite et moins dispendieuse que celle qui est en usage, pour les rendre capables d'une plus longue résistance ; mais en attendant qu'on trouve un système qui réponde à ces vues, il est un moyen bien simple de rendre les places susceptibles d'une plus longue défense sans en augmenter ou changer les fortifications : il ne s'agit pour cela que de ne les confier qu'à des chefs habiles et expérimentés, fort au fait de la place, de l'artillerie et de tout ce qui concerne le génie ; on verra alors ce qu'on peut attendre de la fortification moderne, comme M. Dupuy-Vauban l'a fait voir dans sa belle défense de Béthune. Voyez GUERRE DES SIEGES. (Q)
SYSTEME, en Musique, est tout intervalle composé, ou que l'on conçoit composé d'autres intervalles plus petits ; et ces intervalles premiers, qui sont les éléments du système s'appellent par les Grecs diastêmes. Voyez ce mot.
Il y a une infinité d'intervalles différents ; il y a, par conséquent, autant de systèmes possibles. Pour nous borner ici à quelque chose de réel, nous parlerons seulement des systèmes harmoniques ; c'est-à-dire, de ceux dont les éléments sont, ou des consonnances, ou des intervalles engendrés médiatement ou immédiatement par des consonnances. Voyez INTERVALLES.
Les anciens divisaient les systèmes en systèmes particuliers et en systèmes généraux. Ils appelaient système particulier tout composé d'au-moins deux intervalles, tels que sont l'octave, la quinte, la sixte, et même la tierce. J'ai traité de ceux-ci au mot INTERVALLE.
Les systèmes généraux qu'ils appelaient plus communément diagrammes, étaient formés par la somme de tous les systèmes particuliers, et comprenaient par conséquent tous les sons employés dans la mélopée. C'est de ceux-là qu'il me reste à parler dans cet article.
On doit juger des progrès de l'ancien système par ceux des instruments de musique destinés à l'exécution ; car ces instruments accompagnant la voix, et jouant tout ce qu'elle chantait, devaient nécessairement rendre autant de sons différents qu'il en entrait dans le système. Or les cordes de ces premiers instruments se touchaient à vide ; il y fallait donc autant de cordes que le système renfermait de sons, et c'est ainsi que dès l'origine de la Musique, on peut sur le nombre des cordes de l'instrument déterminer le nombre des sons du système.
Tout le système des Grecs ne fut donc d'abord composé que de quatre cordes qui formaient l'accord de leur lyre ou cithare. Ces quatre sons, selon quelques-uns, formaient des degrés conjoints, selon d'autres, ils n'étaient pas diatoniques, mais les deux extrêmes sonnaient l'octave, et les deux sons moyens la partageaient en une quarte de chaque côté, et en un ton dans le milieu ; de cette manière :
Ut - trite diezeugmenon,
Sol - lichanos meson,
Fa - parypate meson,
Ut - parypate hypaton.
C'est ce que Boèce appelle le tretracorde Mercure.
Ce système ne demeura pas longtemps borné à si peu de sons. Chorèbe, fils d'Athis, roi de Lydie, y ajouta une cinquième corde, Hyagnis une sixième, Terpandre une septième, à l'imitation du nombre des planètes, et enfin Lichaon de Samos la huitième.
Voilà ce que dit Boèce ; mais Pline témoigne que Terpandre ayant ajouté trois cordes aux quatre anciennes, joua le premier de la cithare à sept cordes, que Simonide y en joignit une huitième, et Thimothée une neuvième. Nicomaque le Gérasénien attribue cette huitième corde à Pythagore, la neuvième à Théophraste de Piérie, puis une dixième à Histyée de Colophon, et une onzième à Timothée de Milet, etc. Phérécrate, dans Plutarque, fait faire au système un progrès plus rapide ; il donne douze cordes à la cithare de Mélanippide, et autant à celle de Timothée ; et comme Phérécrate était contemporain de ces musiciens, son témoignage est d'un grand poids sur un fait qu'il avait, pour ainsi dire sous les yeux.
Mais comment pourrait-on à un certain point s'assurer de la vérité parmi tant de contradictions, soit entre les auteurs, soit dans la nature même des faits qu'ils rapportent ? Par exemple, le tétracorde de Mercure donne évidemment l'octave ou le diapazon. Comment donc s'est-il pu faire qu'après l'addition de trois cordes, tout le diagramme se soit trouvé diminué d'un degré et réduit à un intervalle de septième ? c'est pourtant ce que font entendre la plupart des auteurs anciens, et entr'autres Nicomaque, qui dit que Pythagore trouvant tout le système composé seulement de deux tétracordes conjoints qui formaient entre leurs extrêmes un intervalle dissonnant, il le rendit consonnant en divisant ces deux tétracordes par l'intervalle d'un ton, ce qui produisit l'octave.
Quoi qu'il en sait, c'est du-moins une chose certaine que le système des Grecs s'augmenta insensiblement, tant en haut qu'en bas, et qu'il atteignit, et passa même l'étendue du disdiapason, ou de la double octave ; étendue qu'ils appellent systema perfectum, maximum, immuatum, le grand système, le système parfait, immuable par excellence, à cause qu'entre ces extrémités, dont l'intervalle formait une consonnance parfaite, étaient contenues toutes les consonnances simples, doubles, directes et renversées, tous les systèmes particuliers, &, selon eux, les plus grands intervalles qui pussent avoir lieu dans la mélodie.
Ce système était composé de quatre tétracordes ; trois conjoints et un disjoint, et d'un ton de plus, qui fut ajouté au-dessous du tout pour achever la double octave, d'où la corde qui le formait prit le nom de proslambanomene ou d'ajoutée. Cela n'aurait dû produire que quinze sons dans le genre diatonique ; il y en avait pourtant seize. C'est que la disjonction se faisant sentir tantôt entre le second et le troisième, tantôt entre le troisième tétracorde et le quatrième, il arrivait dans le premier cas qu'après le son la, le plus aigu du second tétracorde, suivait en montant le son si qui commençait le troisième ; ou-bien, dans le second cas, que ce même son la commençant lui-même le troisième tétracorde était immédiatement suivi du si bémol ; car le premier degré de chaque tétracorde était toujours d'un semi-ton. Cette différence produisait donc un seizième son, à cause du si naturel qu'on avait d'un côté, et de l'autre le si bémol. Ces seize sons étaient représentés par dix-huit noms, c'est-à dire que l'ut et le re étant, ou les deux derniers sons, ou les sons moyens du troisième tétracorde, selon ces deux différents cas de disjonction, on donnait à chacun de ces deux sons des noms qui marquaient ces diverses circonstances.
Mais comme le son fondamental variait selon le mode, il s'ensuivait pour chaque mode dans le système total, une différence du grave à l'aigu qui multipliait de beaucoup les sons. Car si les divers modes avaient plusieurs sons communs, ils en avaient aussi de particuliers à chacun ou quelques-uns seulement. Ainsi, dans le seul genre diatonique l'étendue de tous les sons admis dans les quinze modes dénombrés par Alypius, est de trois octaves et un ton ; et comme la différence de chaque mode à son voisin était seulement d'un semi-ton, il est évident que tout cet espace gradué de semi-ton en semi-ton, produisait dans le diagramme général la quantité de 39 sons pratiqués dans la musique ancienne. Que si déduisant toutes les repliques des mêmes sons on se renferme dans les bornes d'une seule octave, on la trouvera divisée chromatiquement par douze sons différents, comme dans la musique moderne ; ce qui est de la dernière évidence par l'inspection des tables mises par Meibomius à la tête de l'ouvrage d'Alypius. Ces remarques sont nécessaires pour relever l'erreur de ceux qui s'imaginent, sur la foi de quelques modernes, que toute la musique ancienne n'était composée que de seize sons.
On trouvera, dans nos Pl. de Musiq. une table du système général des Grecs pris dans un seul mode et dans le genre diatonique. A l'égard des genres enharmoniques et chromatiques, les tétracordes s'y trouvaient bien divisés, selon d'autres proportions ; mais comme ils contenaient toujours également quatre sons et trois intervalles consécutifs, de même que dans le genre diatonique, ces sons portaient chacun dans leur genre le même nom que chaque son qui leur correspondait portait dans le diatonique. C'est pourquoi je ne donne point de tables particulières de chacun de ces genres. Voyez GENRE. Les curieux pourront consulter celles que Meibomius a mises à la tête de l'ouvrage d'Aristoxene ; on y en trouvera six, une pour le genre harmonique, trois pour le chromatique, et deux pour le diatonique, selon les diverses modifications de chacun de ces genres.
Ce système demeura à-peu-près dans cet état jusqu'à l'onzième siècle, où Guy d'Arezze y fit des changements considérables. Il ajouta dans le bas une nouvelle corde, qu'il appela hypoproslambanomene, et dans le haut, un cinquième tétracorde qu'il appela le tétracorde des suvaiguès. Outre cela, il inventa, diton, le bémol, nécessaire pour distinguer le si, deuxième note d'un tétracorde conjoint d'avec le si du même tétracorde disjoint, c'est-à-dire qu'il fixa cette signification de la lettre b, que S. Grégoire, avant lui, avait déjà assignée à la note si : car puisqu'il est certain que les Grecs avaient depuis longtemps ces mêmes conjonctions et disjonctions de tétracordes, et par conséquent des signes pour en exprimer chaque degré dans ces deux différents cas, il s'ensuit que ce n'était pas un nouveau son introduit dans ce système par Guy, mais seulement un nouveau nom qu'il donnait à ce son, réduisant ainsi à un même degré ce qui en faisait deux chez les Grecs.
On conçoit aisément que l'invention du contrepoint, à quelque auteur qu'elle soit due, dut bientôt reculer encore les bornes de ce système. Quatre parties doivent avoir bien plus d'étendue qu'une seule. Le système fut fixé à quatre octaves, et c'est l'étendue du clavier de toutes les anciennes orgues. Mais enfin on s'est trouvé gêné par des limites, quelque espace qu'elles pussent avoir ; on les a franchies, on s'est étendu en haut et en bas : on a fait deux claviers à ravalement ; on a démanché sans cesse ; et enfin, on s'est tant donné de licence à cet égard, que le système moderne n'a plus d'autres bornes dans le haut, que le caprice des compositeurs. Comme on ne peut pas de même démancher pour descendre, la plus basse corde des basses ordinaires ne passe pas encore le c sol ut ; mais on trouvera également le moyen de gagner de ce côté-là en baissant le ton du système général : c'est même ce qu'on fait insensiblement ; et je tiens pour une chose certaine que le ton de l'opéra est plus bas aujourd'hui qu'il ne l'était du temps de Lully. Au contraire celui de la musique instrumentale est monté, et ces différences commencent même à devenir assez sensibles pour qu'on s'en aperçoive dans la pratique.
Voyez dans nos Pl. une table générale du grand clavier à ravalement, et de tous les sons qui sont contenus dans l'étendue de cinq octaves. (S)
SYSTEME, (Finance) on a donné très-bien ce nom vers l'an 1720 au projet connu et exécuté par le sieur Law écossais, de mettre dans ce royaume du papier et des billets de banque pour y circuler, et représenter l'argent monnoyé, comme en Angleterre et en Hollande. J'ai Ve plusieurs éloges de ce grand projet, et quelques-uns faits avec éloquence. C'était, dit M. Dutot, un édifice construit par un habîle architecte, mais dont les fondements n'avaient été faits que pour porter trois étages. Sa beauté surpassa même les espérances que l'on en avait conçues, puisqu'il fit mépriser pendant quelques mois l'or et l'argent, espèce de miracle que la postérité ne croira peut-être pas. Cependant, sans égard au bien que la postérité pouvait retirer de cette idée, une puissante cabale formée contre l'architecte, eut assez de crédit pour engager le gouvernement à surcharger ou à élever cet édifice jusqu'à sept étages, en sorte que les fondements ne pouvant supporter cette surcharge, ils s'écroulèrent, et l'édifice tomba de fond en comble. Voilà bien de l'esprit en pure perte.
Je veux croire cependant que le sieur Law en formant une banque, se proposait d'augmenter utilement la circulation publique, de faciliter le commerce, et de simplifier la perception des revenus du roi ; mais comment pouvait-il se flatter dans la disette la plus générale, d'établir une banque de crédit qui eut la confiance de la nation et des étrangers ? Si l'on parut pendant quelques mois donner la préférence des billets de sa banque à l'argent réel, c'était dans la vue de les fondre, et d'en tirer du profit dès qu'ils auraient haussé davantage par le délire de la nation. Enfin, les remboursements du sieur Law n'ont enrichi que des familles nouvelles en ruinant les anciennes, et les débris de son système n'ont produit dans l'état qu'une compagnie exclusive de commerce, dont je laisse à de plus habiles que moi à calculer les avantages rélativement au bien public. (D.J.)
SYSTEME, (Rubanier) se dit en galon pour la fabrication duquel on se sert de deux navettes, l'une de filé d'or ou d'argent pour travailler en-dessus, et l'autre de soie convenable à la couleur pour le dessous ; par ce moyen il ne parait point de filé du tout en-dessous, ce qui épargne considérablement les étoffes d'or ou d'argent.
SYSTEME
- Détails
- Écrit par Auteur anonyme
- Catégorie parente: Science
- Catégorie : Métaphysique
- Affichages : 3015