




La partie des mécaniques qui considère le mouvement des corps, en tant qu'il vient de leur pesanteur, s'appelle quelquefois statique. (Voyez GRAVITE, &c.) par opposition à la partie qui considère les forces mouvantes et leur application, laquelle est nommée par ces mêmes auteurs Mécanique. Mais on appelle plus proprement statique, la partie de la Mécanique qui considère les corps et les puissances dans un état d'équilibre, et Mécanique la partie qui les considère en mouvement. Voyez STATIQUE. Voyez aussi FORCES MOUVANTES, MACHINE, EQUILIBRE, etc.
M. Newton dans la préface de ses principes, remarque qu'on doit distinguer deux sortes de mécaniques, l'une pratique, l'autre rationnelle ou spéculative, qui procede dans ses opérations par des démonstrations exactes ; la mécanique pratique renferme tous les arts manuels qui lui ont donné leur nom. Mais comme les artistes et les ouvriers ont coutume d'opérer avec peu d'exactitude, on a distingué la Mécanique de la Géométrie, en rapportant tout ce qui est exact à la Géométrie, et ce qui l'est moins à la Mécanique. Ainsi cet illustre auteur remarque que les descriptions des lignes et les figures dans la Géométrie, appartiennent à la Mécanique, et que l'objet véritable de la Géométrie est seulement d'en démontrer les propriétés, après en avoir supposé la description. Par conséquent, ajoute-t-il, la Géométrie est fondée sur des pratiques mécaniques, et elle n'est autre chose que cette pratique de la Mécanique universelle, qui explique et qui démontre l'art de mesurer exactement. Mais comme la plupart des arts manuels ont pour objet le mouvement des corps, on a appliqué le nom de Géométrie à la partie qui a l'étendue pour objet, et le nom de Mécanique à celle qui considère le mouvement. La mécanique rationnelle, prise en ce dernier sens, est la science des mouvements qui résultent de quelque force que ce puisse être, et des forces nécessaires pour produire quelque mouvement que ce sait. M. Newton ajoute que les anciens n'ont guère consideré cette science que dans les puissances qui ont rapport aux arts manuels, savoir le levier, la poulie etc. ; et qu'ils n'ont presque considéré la pesanteur que comme une puissance appliquée au poids que l'on veut mouvoir par le moyen d'une machine. L'ouvrage de ce célèbre philosophe, intitulé Principes mathématiques de la Philosophie naturelle, est le premier où on ait traité la Mécanique sous une autre face et avec quelque étendue, en considérant les lois de la pesanteur, du mouvement, des forces centrales et centrifuges, de la résistance des fluides, etc. Au reste comme la mécanique rationnelle tire beaucoup de secours de la Géométrie, la Géométrie en tire aussi quelquefois de la Mécanique, et l'on peut par son moyen abréger souvent la solution de certains problèmes. Par exemple, M. Bernouilli a fait voir que la courbe que forme une chaîne, fixée sur un plan vertical par ses deux extrémités, est celle qui forme la plus grande surface courbe, en tournant autour de son axe ; parce que c'est celle dont le centre de gravité est le plus bas. Voyez dans les Mém. de l'acad. des Scien. de 1714, le mémoire de M. Varignon intitulé, Réflexions sur l'usage que la mécanique peut avoir en Géométrie. Voyez aussi CHAINETTE.
MECHANIQUE, adj. signifie ce qui a rapport à la Mécanique, ou qui se règle par la nature et les lois du mouvement. Voyez MOUVEMENT.
Nous disons dans ce sens, puissances mécaniques, propriétés ou affections mécaniques, principes mécaniques.
Les affections mécaniques sont les propriétés de la matière qui résultent de sa figure, de son volume et de son mouvement actuel. Voyez MATIERE et CORPS.
Les causes mécaniques sont celles qui ont de telles affections pour fondement. Voyez CAUSE.
Solutions mécaniques, ce sont celles qui n'emploient que les mêmes principes. Voyez SOLUTION.
Philosophie mécanique, c'est la même qu'on appelait autrefois corpusculaire, c'est-à-dire celle qui explique les phénomènes de la nature, et les actions des substances corporelles par les principes mécaniques, savoir le mouvement, la pesanteur, la figure, l'arrangement, la disposition, la grandeur ou la petitesse des parties qui composent les corps naturels. Voyez CORPUSCULE et CORPUSCULAIRE, ATTRACTION, GRAVITE, etc.
On donnait autrefois le nom de corpusculaire à la philosophie d'Epicure, à cause des atomes dont ce philosophe prétendait que tout était formé. Aujourd'hui les Newtoniens le donnent par une espèce de dérision à la philosophie cartésienne, qui prétend expliquer tout par la matière subtile, et par des fluides inconnus, à l'action desquels elle attribue tous les phénomènes de la nature.
Puissances mécaniques, appelées plus proprement forces mouvantes, sont les six machines simples auxquelles toutes les autres, quelque composées qu'elles soient, peuvent se réduire, ou de l'assemblage desquelles toutes les autres sont composées. Voyez PUISSANCE et MACHINE.
Les puissances mécaniques sont le levier, le treuile, la poulie, le plan incliné, le coin, et la vis. Voyez les articles qui leur sont propres, BALANCE, LEVIER, etc. On peut cependant les réduire à une seule, savoir le levier, si on en excepte le plan incliné qui ne s'y réduit pas si sensiblement. M. Varignon a ajouté à ces six machines simples, la machine funiculaire, ou les poids suspendus par des cordes, et tirés par plusieurs puissances.
Le principe dont ces machines dépendent est le même pour toutes, et peut s'expliquer de la manière suivante.
La quantité de mouvement d'un corps, est le produit de sa vitesse, c'est-à-dire de l'espace qu'il parcourt dans un temps donné, par sa masse ; il s'ensuit de-là que deux corps inégaux auront des quantités de mouvement égales, si les lignes qu'ils parcourent en même temps sont réciproquement proportionnelles à leurs masses, c'est-à-dire si l'espace que parcourt le plus grand, dans une seconde par exemple, est à l'espace que parcourt le plus petit dans la même seconde, comme le plus petit corps est au plus grand. Ainsi, supposons deux corps attachés aux extrémités d'une balance ou d'un levier, si ces corps ou leurs masses, sont en raison réciproque de leurs distances de l'appui, ils seront aussi en raison réciproque des lignes ou arcs de cercle qu'ils parcouraient en même temps, si l'on faisait tourner le levier sur son appui ; et par conséquent ils auraient alors des quantités de mouvement égales, ou, comme s'expriment la plupart des auteurs, des moments égaux.
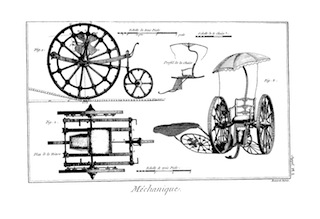
Par exemple, si le corps A (Pl. mech. fig. 4.) est triple du corps B, et que dans cette supposition on attache les deux corps aux deux extrémités d'un levier A B, dont l'appui soit placé en C, de façon que la distance B C soit triple de la distance A C, il s'ensuivra de-là qu'on ne pourra faire tourner le levier sans que l'espace B E, parcouru par le corps situé en B se trouve triple de l'espace A D parcouru en même temps par le corps élevé en A, c'est-à-dire, sans que la vitesse de B ne devienne triple de celle de A, ou enfin sans que les vitesses des deux corps dans ce mouvement soient réciproques à leurs masses. Ainsi les quantités de mouvement des deux corps seront égales ; et comme ils tendent à produire des mouvements contraires dans le levier, le mouvement du levier deviendra par cette raison absolument impossible dans le cas dont nous parlons ; c'est-à-dire qu'il y aura équilibre entre les deux corps. Voyez EQUILIBRE, LEVIER et MOUVEMENT.
De-là ce fameux problême d'Archimède, datis viribus, datum pondus movère. En effet, puisque la distance C B peut être accrue à l'infini, la puissance ou le moment de A, peut donc aussi être supposé aussi grand qu'on voudra par rapport à celui de B, sans empêcher la possibilité de l'équilibre. Or quand une fois on aura trouvé le point où doit être placé le corps B pour faire équilibre au corps A, on n'aura qu'à reculer un peu le corps B, et alors ce corps B, quelque petit qu'il sait, obligera le corps A de se mouvoir. Voyez MOMENT. Ainsi toutes les mécaniques peuvent se réduire au problême suivant.
Un corps A avec sa vitesse C, et un autre corps B étant donnés, trouver la vitesse qu'il faut donner à B, pour que les deux corps aient des moments égaux. Pour résoudre ce problême, on remarquera que puisque le moment d'un corps est égal au produit de sa vitesse, par la quantité de matière qu'il contient, il n'y a donc qu'à faire cette proportion, B : A : : C : à un quatrième terme, et ce sera la vitesse cherchée qu'il faudra donner au corps B, pour que son moment soit égal à celui de A. Aussi dans quelques machines que ce sait, si l'on fait en sorte que la puissance ou la force, ne puisse agir sur la résistance ou le poids, ou les vaincre actuellement sans que dans cette action les vitesses de la puissance et du poids soient réciproques à leur masse, alors le mouvement deviendra absolument impossible. La force de la puissance ne pourra vaincre la résistance du poids, et ne devra pas non plus lui céder ; et par conséquent la puissance et le poids resteront en équilibre sur cette machine, et si on augmente tant-sait-peu la puissance, elle enlevera alors le poids ; mais si on augmentait au contraire le poids, il entraînerait la puissance.
Supposons, par exemple, que A B soit un levier, dont l'appui soit placé en C, et qu'en tournant autour de cet appui, il soit parvenu à la situation a, C, b (fig. 1. Mécan.) la vitesse de chaque point du levier aura été évidemment dans ce mouvement proportionnelle à la distance de ce point à l'appui ou centre de la circulation. Car les vitesses de chaque point sont comme les arcs que ces points ont décrits en même temps, lesquels sont d'un même nombre de degrés. Ces vitesses sont donc aussi entr'elles comme les rayons des arcs de cercles par chaque point du levier, c'est-à-dire, comme les distances de chaque point à l'appui.
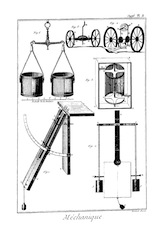
Si l'on suppose maintenant deux puissances appliquées aux deux extrémités du levier et qui fassent tout-à-la-fais effort pour faire tourner ses bras dans un sens contraire l'un à l'autre, et que ces puissances soient réciproquement proportionnelles à leur distance de l'appui, il est évident que le moment ou effort de l'une pour faire tourner le levier en un sens, sera précisément égal au moment de l'autre pour le faire tourner en sens contraire. Il n'y aura donc pas plus de raisons, pour que le levier tourne dans un sens que dans le sens opposé. Il restera donc nécessairement en repos, et il y aura équilibre entre les deux puissances : c'est ce qu'on voit tous les jours, lorsqu'on pese un poids avec une romaine. Il est aisé de concevoir par ce que nous venons de dire, comment un poids d'une livre peut sur cette machine faire équilibre avec un poids de mille livres et davantage.
C'est par cette raison qu'Archimède ne demandait qu'un point fixe hors de la terre, pour l'enlever. Car, en faisant de ce point fixe l'appui d'un levier, et mettant la terre à l'extrémité d'un des bras de ce levier, il est clair qu'en allongeant l'autre bras, on parviendrait à mouvoir le globe terrestre avec une force aussi petite qu'on voudrait. Mais on sent bien que cette proposition d'Archimède n'est vraie que dans la spéculation ; puisqu'on ne trouvera jamais ni le point fixe qu'il demandait, ni un levier de la longueur nécessaire pour mouvoir le globe terrestre.
Il est clair encore par-là que la force de la puissance n'est point-du-tout augmentée par la machine, mais que l'application de l'instrument diminue la vitesse du poids dans son élévation ou dans sa traction, par rapport à celle de la puissance dans son action ; de sorte qu'on vient à bout de rendre le moment d'une petite puissance égal, et même supérieur à celui d'un gros poids, et que par-là on parvient à faire enlever ou trainer le gros poids par la petite puissance. Si, par exemple, une puissance est capable d'enlever un poids d'une livre, en lui donnant dans son élévation un certain degré de vitesse, on ne fera jamais par le secours de quelque machine que ce puisse être que cette même force puisse enlever un poids de deux livres, en lui donnant dans son élévation la même vitesse dont nous venons de parler. Mais on viendra facilement à bout de faire enlever à la puissance le poids de deux livres, avec une vitesse deux fois moindre, ou, si l'on veut, un poids de dix mille livres, avec une vitesse dix mille fois moindre.
Plusieurs auteurs ont tenté d'appliquer les principes de la Mécanique au corps humain ; il est cependant bon d'observer que l'application des principes de la Mécanique à cet objet ne se doit faire qu'avec une extrême précaution. Cette machine est si compliquée, que l'on risque souvent de tomber dans bien des erreurs, en voulant déterminer les forces qui la font agir ; parce que nous ne connaissons que très-imparfaitement la structure et la nature des différentes parties que ces forces doivent mouvoir. Plusieurs médecins et physiciens, surtout parmi les Anglais, sont tombés dans l'inconvénient dont je parle ici. Ils ont prétendu donner, par exemple, les lois du mouvement du sang, et de son action sur les vaisseaux ; et ils n'ont pas pris garde, que pour réussir dans une telle recherche, il serait nécessaire de connaître auparavant une infinité de choses qui nous sont cachées, comme la figure des vaisseaux, leur élasticité, le nombre, la force et la disposition de leurs valvules, le degré de chaleur et de tenacité du sang, les forces motrices qui le poussent, etc. Encore, quand chacune de ces choses serait parfaitement connue, la grande quantité d'éléments qui entreraient dans une pareille théorie, nous conduirait vraisemblablement à des calculs impraticables. Voyez LE DISCOURS PRELIMINAIRE.
MECHANIQUE, (Mathématiques) est encore d'usage en Mathématiques, pour marquer une construction ou solution de quelque problème qui n'est point géométrique, c'est-à-dire, dont on ne peut venir à bout par des descriptions de courbes géométriques. Telles sont les constructions qui dépendent de la quadrature du cercle. Voyez CONSTRUCTION, QUADRATURE, etc. Voyez aussi GEOMETRIQUE.
Arts mécaniques. Voyez ART.
Courbe mécanique, terme que Descartes a mis en usage pour marquer une courbe qui ne peut pas être exprimée par une équation algébrique. Ces courbes sont par-là opposées aux courbes algébriques ou géométriques. Voyez COURBE.
M. Leibnitz et quelques autres les appellent transcendantes au lieu de mécaniques, et ils ne conviennent pas avec Descartes qu'il faille les exclure de la Géométrie.
Le cercle, les sections coniques, etc. sont des courbes géométriques, parce que la relation de leurs absides à leurs ordonnées est exprimée en termes finis. Mais la cycloïde, la spirale, et une infinité d'autres sont des courbes mécaniques, parce qu'on ne peut avoir la relation de leurs absides à leurs ordonnées que par des équations différentielles, c'est-à-dire, qui contiennent des quantités infiniment petites. Voyez DIFFERENTIELLE, FLUXION, TANGENTE, EXPONENTIELLE, etc. (O).
Les vérités fondamentales de la Mécanique, en tant qu'elle traite des lois du mouvement, et de l'équilibre des corps, méritent d'être approfondies avec soin. Il semble qu'on n'a pas été jusqu'à présent fort attentif ni à réduire les principes de cette science au plus petit nombre, ni à leur donner toute la clarté qu'on pouvait désirer ; aussi la plupart de ces principes, ou obscurs par eux-mêmes, ou énoncés et démontrés d'une manière obscure, ont-ils donné lieu à plusieurs questions épineuses. En général on a été plus occupé jusqu'à présent à augmenter l'édifice, qu'à en éclairer l'entrée, et on a pensé principalement à l'élever, sans donner à ses fondements toute la solidité convenable.
Il nous parait qu'en applaudissant l'abord de cette science, on en reculerait en même-temps les limites, c'est-à-dire qu'on peut faire voir tout à la fois et l'inutilité de plusieurs principes employés jusqu'à présent par les Mécaniciens, et l'avantage qu'on peut tirer de la combinaison des autres, pour le progrès de cette science ; en un mot, qu'en réduisant les principes on les étendra. En effet, plus ils seront en petit nombre, plus ils doivent avoir d'étendue, puisque l'objet d'une science étant nécessairement déterminé, les principes en doivent être d'autant plus féconds, qu'ils sont moins nombreux. Pour faire connaître au lecteur les moyens par lesquels on peut espérer de remplir les vues que nous proposons, il ne sera peut-être pas inutîle d'entrer ici dans un examen raisonné de la science dont il s'agit.
Le mouvement et ses propriétés générales sont le premier et le principal objet de la mécanique ; cette science suppose l'existence du mouvement, et nous la supposerons aussi comme avouée et reconnue de tous les Physiciens. A l'égard de la nature du mouvement, les Philosophes sont au contraire fort partagés là-dessus. Rien n'est plus naturel, je l'avoue, que de concevoir le mouvement comme l'application successive du mobîle aux différentes parties de l'espace indéfini que nous imaginons comme le lieu des corps ; mais cette idée suppose un espace dont les parties soient pénétrables et immobiles ; or personne n'ignore que les Cartésiens (secte à la vérité fort affoiblie aujourd'hui) ne reconnaissent point d'espace distingué des corps, et qu'ils regardent l'étendue et la matière comme une même chose. Il faut convenir qu'en partant d'un pareil principe, le mouvement serait la chose la plus difficîle à concevoir, et qu'un cartésien aurait peut-être beaucoup plutôt fait d'en nier l'existance, que de chercher à en définir la nature. Au reste, quelque absurde que nous paraisse l'opinion de ces philosophes, et quelque peu de clarté et de précision qu'il y ait dans les principes métaphysiques sur lesquels ils s'efforcent de l'appuyer, nous n'entreprendrons point de la refuter ici : nous nous contenterons de remarquer que pour avoir une idée claire du mouvement, on ne peut se dispenser de distinguer au-moins par l'esprit deux sortes d'étendue ; l'une qui soit regardée comme impénétrable, et qui constitue ce qu'on appelle proprement les corps ; l'autre, qui étant considérée simplement comme étendue, sans examiner si elle est pénétrable ou non, soit la mesure de la distance d'un corps à un autre, et dont les parties envisagées comme fixes et immobiles, puissent servir à juger du repos ou du mouvement des corps. Il nous sera donc toujours permis de concevoir un espace indéfini comme le lieu des corps, soit réel, soit supposé, et de regarder le mouvement comme le transport du mobîle d'un lieu dans un autre.
La considération du mouvement entre quelquefois dans les recherches de la Géométrie pure ; c'est ainsi qu'on imagine souvent les lignes droites ou courbes engendrées par le mouvement continu d'un point, les surfaces par le mouvement d'une ligne, les solides enfin par celui d'une surface. Mais il y a entre la Mécanique et la Géométrie cette différence, non seulement que dans celle-ci la génération des figures par le mouvement est pour ainsi dire arbitraire et de pure élégance, mais encore que la Géométrie ne considère dans le mouvement que l'espace parcouru, au lieu que dans la Mécanique on a égard de plus au temps que le mobîle emploie à parcourir cet espace.
On ne peut comparer ensemble deux choses d'une nature différente, telles que l'espace et le temps : mais on peut comparer le rapport des parties du temps, avec celui des parties de l'espace parcouru. Le temps par sa nature coule uniformément, et la Mécanique suppose cette uniformité. Du reste, sans connaître le temps en lui-même, et sans avoir de mesure précise, nous ne pouvons représenter plus clairement le rapport de ses parties, que par celui des portions d'une ligne droite indéfinie. Or l'analogie qu'il y a entre le rapport des parties d'une telle ligne, et celui des parties de l'espace parcouru par un corps qui se meut d'une manière quelconque, peut toujours être exprimée par une équation. On peut donc imaginer une courbe, dont les abscisses représentent les portions du temps écoulé depuis le commencement du mouvement, les ordonnées correspondantes désignant les espaces parcourus durant ces portions de temps : l'équation de cette courbe exprimera non le rapport des temps aux espaces, mais si on peut parler ainsi, le rapport du rapport que les parties de temps ont à leur unité, à celui que les parties de l'espace parcouru ont à la leur. Car l'équation d'une courbe peut être considérée ou comme exprimant le rapport des ordonnées aux abscisses, ou comme l'équation entre le rapport que les ordonnées ont à leur unité, et le rapport que les abscisses correspondantes ont à la leur.
Il est donc évident que par l'application seule de la Géométrie et du calcul, on peut, sans le secours d'aucun autre principe, trouver les propriétés générales du mouvement, varié suivant une loi quelconque. Mais comment arrive-t-il que le mouvement d'un corps suive telle ou telle loi particulière ? C'est sur quoi la Géométrie seule ne peut rien nous apprendre ; et c'est aussi ce qu'on peut regarder comme le premier problème qui appartienne immédiatement à la Mécanique.
On voit d'abord fort clairement qu'un corps ne peut se donner le mouvement à lui-même. Il ne peut donc être tiré du repos que par l'action de quelque cause étrangère. Mais continue-t-il à se mouvoir de lui-même, ou a-t-il besoin pour se mouvoir de l'action répétée de la cause ? Quelque parti qu'on put prendre là-dessus, il sera toujours incontestable que l'existence du mouvement étant une fois supposée sans aucune autre hypothèse particulière, la loi la plus simple qu'un mobîle puisse observer dans son mouvement, est la loi d'uniformité, et c'est par conséquent celle qu'il doit suivre.
Le mouvement est donc uniforme par sa nature ; j'avoue que les preuves qu'on a données jusqu'à-présent de ce principe, ne sont peut-être pas fort convaincantes. On verra à l'article FORCE D'INERTIE, les difficultés qu'on peut y opposer, et le chemin que j'ai pris pour éviter de m'engager à les résoudre. Il me semble que cette loi d'uniformité essentielle au mouvement considéré en lui-même, fournit une des meilleures raisons sur lesquelles la mesure du temps par le mouvement uniforme, puisse être appuyée. Voyez UNIFORME.
La force d'inertie, c'est-à-dire la propriété qu'ont les corps de persévérer dans leur état de repos ou de mouvement, étant une fois établie, il est clair que le mouvement qui a besoin d'une course pour commencer au-moins à exister, ne saurait non plus être accéléré ou retardé que par une cause étrangère. Or quelles sont les causes capables de produire ou de changer le mouvement dans les corps ? Nous n'en connaissons jusqu'à-présent que de deux sortes ; les unes se manifestent à nous en même temps que l'effet qu'elles produisent, ou plutôt dont elles sont l'occasion : ce sont celles qui ont leur source dans l'action sensible et mutuelle des corps, résultante de leur impénétrabilité ; elles se réduisent à l'impulsion et à quelqu'autres actions dérivées de celles-là : toutes les autres causes ne se font connaître que par leur effet, et nous en ignorons entièrement la nature : telle est la cause qui fait tomber les corps pesans vers le centre de la terre, celle qui retient les planètes dans leurs orbites, etc.
Nous verrons bien-tôt comment on peut déterminer les effets de l'impulsion et des causes qui peuvent s'y rapporter : pour nous en tenir ici à celles de la seconde espèce, il est clair que lorsqu'il est question des effets produits par de telles causes, ces effets doivent toujours être donnés indépendamment de la connaissance de la cause, puisqu'ils ne peuvent en être déduits ; sur quoi voyez ACCELERATRICE.
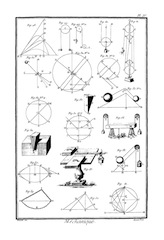
Nous n'avons fait mention jusqu'à-présent, que du changement produit dans la vitesse du mobîle par les causes capables d'altérer son mouvement : et nous n'avons point encore cherché ce qui doit arriver, si la cause motrice tend à mouvoir le corps dans une direction différente de celle qu'il a déjà. Tout ce que nous apprend dans ce cas le principe de la force d'inertie, c'est que le mobîle ne peut tendre qu'à décrire une ligne droite, et à la décrire uniformément : mais cela ne fait connaître ni sa vitesse, ni sa direction. On est donc obligé d'avoir recours à un second principe, c'est celui qu'on appelle la composition des mouvements, et par lequel on détermine le mouvement unique d'un corps qui tend à se mouvoir suivant différentes directions à la fois avec des vitesses données. Voyez COMPOSITION DU MOUVEMENT.
Comme le mouvement d'un corps qui change de direction, peut être regardé comme composé du mouvement qu'il avait d'abord, et d'un nouveau mouvement qu'il a reçu, de même le mouvement que le corps avait d'abord peut être regardé comme composé du nouveau mouvement qu'il a pris, et d'un autre qu'il a perdu. De-là il s'ensuit, que les lois du mouvement changé par quelques obstacles que ce puisse être, dépendent uniquement des lois du mouvement, détruit par ces mêmes obstacles. Car il est évident qu'il suffit de décomposer le mouvement qu'avait le corps avant la rencontre de l'obstacle, en deux autres mouvements, tels que l'obstacle ne nuise point à l'un, et qu'il anéantisse l'autre. Par-là, on peut non-seulement démontrer les lois du mouvement changé par des obstacles insurmontables, les seules qu'on ait trouvées jusqu'à présent par cette méthode ; on peut encore déterminer dans quel cas le mouvement est détruit par ces mêmes obstacles. A l'égard des lois du mouvement changé par des obstacles qui ne sont pas insurmontables en eux-mêmes, il est clair par la même raison, qu'en général il ne faut point déterminer ces lais, qu'après avoir bien constaté celles de l'équilibre. Voyez ÉQUILIBRE.
Le principe de l'équilibre joint à ceux de la force d'inertie et du mouvement composé, nous conduit donc à la solution de tous les problèmes où l'on considère le mouvement d'un corps, en tant qu'il peut être altéré par un obstacle impénétrable et mobile, c'est-à-dire en général par un autre corps à qui il doit nécessairement communiquer du mouvement pour conserver au moins une partie du sien. De ces principes combinés, on peut donc aisément déduire les lois du mouvement des corps qui se choquent d'une manière quelconque, ou qui se tirent par le moyen de quelque corps interposé entr'eux, et auquel ils sont attachés : lois aussi certaines et de vérité aussi nécessaire, que celles du mouvement des corps altéré par des obstacles insurmontables, puisque les unes et les autres se déterminent par les mêmes méthodes.
Si les principes de la force d'inertie, du mouvement composé, et de l'équilibre, sont essentiellement différents l'un de l'autre, comme on ne peut s'empêcher d'en convenir ; et si d'un autre côté, ces trois principes suffisent à la Mécanique, c'est avoir réduit cette science au plus petit nombre de principes possibles, que d'avoir établi sur ces trois principes toutes les lois du mouvement des corps dans des circonstances quelconques, comme j'ai tâché de le faire dans mon traité.
A l'égard des démonstrations de ces principes en eux-mêmes, le plan que l'on doit suivre pour leur donner toute la clarté et la simplicité dont elles sont susceptibles, a été de les déduire toujours de la considération seule du mouvement, envisagé de la manière la plus simple et la plus claire. Tout ce que nous voyons bien distinctement dans le mouvement d'un corps, c'est qu'il parcourt un certain espace, et qu'il emploie un certain temps à le parcourir. C'est donc de cette seule idée qu'on doit tirer tous les principes de la Mécanique, quand on veut les démontrer d'une manière nette et précise ; en conséquence de cette réflexion, le philosophe doit pour ainsi dire, détourner la vue de dessus les causes motrices, pour n'envisager uniquement que le mouvement qu'elles produisent ; il doit entièrement proscrire les forces inhérentes au corps en mouvement, êtres obscurs et métaphysiques, qui ne sont capables que de répandre les ténèbres sur une science claire par elle-même. Voyez FORCE.
Les anciens, comme nous l'avons déjà insinué plus haut, d'après M. Newton, n'ont cultivé la Mécanique que par rapport à la statique ; et parmi eux Archimède s'est distingué sur ce sujet par ses deux traités de aequiponderantibus, etc. incidentibus humido. Il était réservé aux modernes, non-seulement d'ajouter aux découvertes des anciens touchant la statique, voyez STATIQUE ; mais encore de créer une science nouvelle sous le titre de Mécanique proprement dite, ou de la science des corps et mouvements. On doit à Stevin, mathématicien du prince d'Orange, le principe de la composition des forces que M. Varignon a depuis heureusement appliqué à l'équilibre des machines ; à Galilée, la théorie de l'accélération, voyez ACCELERATION et DESCENTE ; à MM. Huygens, Wren et Wallis, les lois de la percussion, voyez PERCUSSION et COMMUNICATION DU MOUVEMENT ; à M. Huygens les lois des forces centrales dans le cercle ; à M. Newton, l'extension de ces lois aux autres courbes et au système du monde, voyez CENTRALE et FORCE ; enfin aux géomètres de ce siècle la théorie de la dynamique. Voyez DYNAMIQUE et HYDRODYNAMIQUE. (O)

