LONGITUDE d’une étoile, s. f. (Astronomie) est un arc de l’écliptique compris depuis le premier point d’aries, jusqu’à l’endrait où le cercle de latitude de l’étoîle coupe l’écliptique.
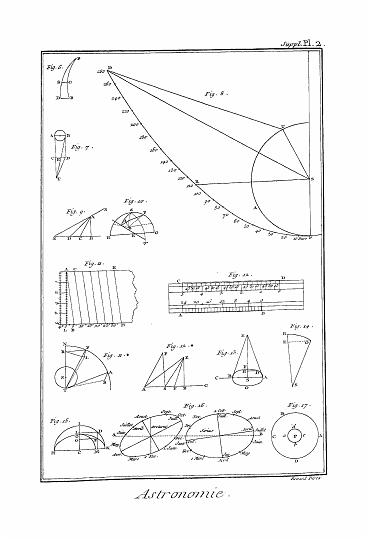
Ainsi, la longitude d'une étoîle comme S, (Pl. d'Ast. fig. 32.) est un arc de l'écliptique T L, compris entre le commencement d'aries, et le cercle de latitude T M, qui passe par le centre S de l'étoile, et par les pôles de l'écliptique.
La longitude est par rapport à l'écliptique ce que l'ascension droite est par rapport à l'équateur. Voyez ASCENSION.
Dans ce sens la longitude d'une étoîle n'est autre chose que son lieu dans l'écliptique, à compter depuis le commencement d'aries.
Pour trouver la longitude d'une étoile, ainsi que sa latitude, la difficulté se réduit à trouver son inclinaison et son ascension droite. Voyez ces deux mots ; car connaissant ces deux derniers, et connaissant de plus l'angle de l'équateur avec l'écliptique, et l'endroit où l'écliptique coupe l'équateur, il est visible qu'on aura par les seules règles de la Trigonométrie sphérique la longitude et la latitude de l'étoile. Or nous avons donné et indiqué aux mots DECLINAISON, ÉTOILE, ASCENSION et GLOBE, les différents moyens de trouver l'ascension droite et la déclinaison des étoiles ou des planètes.
La longitude du soleil ou d'une étoîle depuis le point équinoxial le plus proche de l'étoile, c'est le nombre de degrés, de minutes qu'il y a du commencement d'aries ou de libra, jusqu'au soleil ou à l'étoile, soit en avant, soit en arrière, et cette distance ne peut jamais être de plus de 180 degrés.
Longitude d'un lieu, en Géographie, c'est la distance de ce lieu à un méridien qu'on regarde comme le premier ; ou un arc de l'équateur, compris entre le méridien du lieu et le premier méridien. Voyez MERIDIEN.
Le premier méridien était autrefois placé à l'île de Fer, la plus occidentale des Canaries, et Louis XIII. l'avait ainsi ordonné pour rendre la Géographie plus simple ; aujourd'hui presque tous les Géographes et les Astronomes comptent les longitudes de leur méridien, c'est-à-dire du méridien du lieu où ils observent : cela est assez indifférent en soi ; car il est égal de prendre pour premier méridien un méridien ou un autre, et on aura toujours la longitude d'un endroit de la terre lorsqu'on aura la position de son méridien par rapport au méridien de quelque autre lieu, comme Paris, Londres, Rome, etc. Il est pourrant vrai que si tous les Astronomes convenaient d'un méridien commun, on ne serait point obligé de faire des réductions qui sont nécessaires pour ne pas embrouiller la géographie moderne. On peut en général définir la longitude, le nombre de degrés de l'équateur compris entre le méridien du lieu et celui de tout autre lieu proposé. Vous voulez savoir, par exemple, de combien Pekin, capitale de la Chine, est éloignée de Paris en longitude, amenez Paris sous le méridien commun, et éloignez ensuite ce point vers l'occident, en comptant combien il passe de degrés de l'équateur sous le méridien, jusqu'à ce que vous aperceviez Pekin arrivé sous le méridien ; suivant le grand globe de M. Delille, vous trouverez 113 degrés de l'équateur, écoulés entre le méridien de Paris et celui de Pekin.
Dans la numération des degrés, le pôle arctique étant toujours vers le haut, la distance qui s'étend à droite jusqu'à 180 degrés, marque de combien un lieu proposé est plus oriental qu'un autre. La distance qui s'étend de même à gauche jusqu'à 180 degrés, marque de combien un lieu est plus occidental qu'un autre. Ce serait une commodité d'appeler longitude orientale les degrés qui sont à droite du méridien d'un lieu, jusqu'au nombre de 180 degrés, et longitude occidentale ceux qui s'étendent à la gauche du même méridien, en pareil nombre : mais c'est un usage universel de ne compter qu'une seule progression de longitude jusqu'à 360 degrés.
Longitude, en Navigation, c'est la distance du vaisseau, ou du lieu où on est à un autre lieu, compté de l'est à l'ouest, en degrés de l'équateur.
La longitude de deux lieux sur mer peut s'estimer de quatre manières ; ou par l'arc de l'équateur compris entre les méridiens de ces deux lieux ; ou par l'arc du parallèle qui passe par le premier de ces lieux, et qui est terminé par les deux méridiens ; ou par l'arc du parallèle compris entre les deux méridiens, et qui passe par le second de ces deux lieux ; ou enfin par la somme des arcs de différents parallèles compris entre les différents méridiens qui divisent l'espace compris entre les deux méridiens. Or de quelque manière qu'on s'y prenne il faudra toujours estimer la distance des méridiens en degrés, et il parait plus commode de la marquer par des degrés de l'équateur qu'autrement. Mais il faut remarquer que ces degrés ne donnent point la distance des deux lieux : car tous les arcs, soit de l'équateur, soit des parallèles compris entre les mêmes méridiens, ont le même nombre de degrés, et tous les lieux situés sous ces méridiens ont la même différence de longitude, mais ils sont d'autant plus proches les uns des autres qu'ils sont plus près du pôle ; c'est à quoi il faut avoir égard en calculant les distances des lieux dont les longitudes et les latitudes sont communes, et les marins ont des tables toutes dressées pour cela.
La recherche d'une méthode exacte pour trouver les longitudes en mer, est un problême qui a beaucoup exercé les Mathématiciens des deux derniers siècles, et pour la solution duquel les Anglais ont proposé publiquement de grandes récompenses : on a fait de vains efforts pour en venir à bout, et on a proposé différentes méthodes, mais sans succès ; les projets se sont toujours trouvés mauvais, supposant des opérations trop impraticables, ou vicieuses par quelque endroit ; de façon que la palme n'a encore été déférée à personne.
L'objet que la plupart se proposent, est de trouver une différence de temps entre deux points quelconques de la terre : car il répond une heure à 15 degrés de l'équateur, c'est-à-dire, 4 minutes de temps à chaque degré de l'équateur, 4 secondes de temps à chaque minute de degré ; et ainsi la différence de temps étant connue et convertie en degrés, elle donnerait la longitude, et réciproquement.
Pour découvrir la différence de temps, on s'est servi d'horloges, de montres et d'autres machines, mais toujours en vain, n'y ayant, de tous les instruments propres à marquer le temps, que la seule pendule qui soit assez exacte pour cet effet, et la pendule ne pouvant être d'usage à la mer. D'autres avec des vues plus saines, et plus de probabilité de succès, vont chercher dans les cieux les moyens de découvrir les longitudes sur terre. En effet, si l'on connait pour deux différents endroits les temps exacts de quelque apparence céleste, la différence de ces deux temps donnera la différence des longitudes entre ces deux lieux. Or nous avons dans les éphémérides les mouvements des planètes, et les temps de tous les phénomènes célestes, comme les commencements et les fins des éclipses, les conjonctions de la lune avec les autres planètes dans l'écliptique calculées pour un certain lieu. Si donc on pouvait observer exactement l'heure et la minute dans laquelle ces phénomènes arrivent dans un autre lieu quelconque, la différence de temps entre ces momens-là et celui qui est marqué dans les tables étant convertie en degrés, donnerait la différence de longitude entre le lieu où l'on fait l'observation et celui pour lequel les tables ont été construites.
La difficulté ne consiste pas à trouver exactement l'heure qu'il est, on en vient à bout par les observations de la hauteur du soleil ; mais ce qui manque, c'est un nombre suffisant d'apparences qui puissent être observées ; car tous ces mouvements lents, par exemple, celui de saturne, sont d'abord exclus, parce qu'une petite différence d'apparence ne s'y laisse apercevoir que dans un grand espace de temps, et qu'il faut ici que le phénomène varie sensiblement en deux minutes de temps au plus, une erreur de deux minutes sur le temps en produisant une de trente mille dans la longitude. Or parmi les phénomènes qui se trouvent dans ce cas, ceux qui ont paru les plus propres à cet objet, sont les différentes phases des éclipses de la lune, la longitude de cet astre ou son lieu dans le zodiaque, sa distance des étoiles fixes, ou le mouvement où elle se joint à elles, et la conjonction, la distance et les éclipses des satellites de Jupiter : nous allons parler de chacun de ces moyens l'un après l'autre.
1°. La méthode par les éclipses de lune est très-aisée, et serait assez exacte s'il y avait des éclipses de lune chaque nuit. Au moment que nous voyons le commencement ou le milieu d'une éclipse de lune, nous n'avons qu'à prendre la hauteur ou le zénith de quelque étoîle fixe, et nous en conclurons l'heure, cela suppose que nous connaissons d'ailleurs la latitude, et alors il n'y aura qu'à résoudre un triangle sphérique dont les trois côtés sont connus, savoir le premier, la distance du zénith au pôle, complément de la latitude ; le second, celle de l'étoîle au zénith, complément de la hauteur de l'étoîle ; le troisième, celle de l'étoîle au pôle, complement de la déclinaison de l'étoile, car on tirera de-là la valeur de l'angle formé par le méridien et le cercle de déclinaison passant par l'étoile, ce qui ajouté à la différence d'ascension droite du soleil et de l'astre pour ce jour-là, donnera la distance du soleil au méridien, ou le temps qu'on cherche, c'est-à-dire, l'heure du jour au moment et au lieu de l'observation ; on n'aurait pas même besoin de connaître la hauteur de l'étoile, si l'étoîle était dans le méridien. En effet, l'heure du moment de l'observation sera donnée alors par la seule différence d'ascension droite de l'oeil et de l'étoîle pour ce jour-là, convertie en temps ; ce moment qu'on aura trouvé de la sorte, étant comparé à celui qui est marqué dans les tables pour la même éclipse, nous donnera la longitude. Voyez ÉCLIPSE.
2°. Le lieu de la lune dans le zodiaque n'est pas un phénomène qui ait, comme ce dernier, le défaut de ne pouvoir être observé que rarement ; mais en revanche l'observation en est difficile, et le calcul compliqué et embarrassé à cause de deux parallaxes auxquelles il faut avoir égard ; de sorte qu'à peine peut-on se servir de ce phénomène avec la moindre assurance, pour déterminer les longitudes. Il est vrai que si l'on attend que la lune passe au méridien du lieu, et qu'on prenne alors la hauteur de quelque étoîle remarquable (on suppose qu'on a connu déjà la latitude du lieu) la latitude déduira assez exactement le temps, quoiqu'il fût mieux encore d'employer à cela l'observation de quelques étoiles situées dans le méridien.
Or le temps étant trouvé, il sera aisé de connaître quel point de l'écliptique passe alors par le méridien, et par-là nous aurons le lieu de la lune dans le zodiaque correspondant au temps de l'endroit où nous nous trouvons ; nous chercherons alors dans les éphémérides à quelle heure du méridien des éphémérides la lune doit se trouver dans le même point du zodiaque, et nous aurons ainsi les heures des deux lieux dans le même instant, enfin leur différence convertie en degrés de grand cercle, nous donnera la longitude.
3°. Comme il arrive souvent que la lune doit être observée dans le méridien, les Astronomes ont tourné pour cette raison leurs vues du côté d'un autre phénomène plus fréquent pour en déduire les longitudes, c'est l'occultation des étoiles fixes par la lune ; en effet, l'entrée des étoiles dans le disque de la lune, ou leur sortie de ce disque, peut déterminer le vrai lieu de la lune dans le ciel pour le moment donné de l'observation ; mais les parallaxes auxquelles il faut avoir égard, ces triangles sphériques obliquangles qu'il faut résoudre, et la variété des cas qui peuvent se présenter, rendent cette méthode si difficîle et si compliquée, que les gens de mer n'en ont fait que très-peu d'usage jusqu'à présent. Ceux qui voudront s'en servir trouveront un grand secours dans le zodiaque des étoiles, publié par les soins du docteur Halley, et qui contient toutes les étoiles dont on peut observer les occultations par la lune.
Mais malgré le peu d'usage qu'on a fait jusqu'ici de cette méthode, la plupart des plus habiles astronomes de ce siècle craient que l'observation de la lune est peut-être le moyen le plus exact de découvrir les longitudes. Il n'est pas nécessaire, selon eux, d'observer l'occultation des étoiles par la lune pour marquer un instant déterminé ; le mouvement de la lune est si rapide, que si on rapporte sa situation à deux étoiles fixes, elle forme avec ces étoiles un triangle qui, changeant continuellement de figure, peut être pris pour un phénomène instantané, et déterminer le moment auquel on l'observe. Il n'y a plus d'heure de la nuit, il n'y a plus d'heure où la lune et les étoiles soient visibles, qui n'offre à nos yeux un tel phénomène ; et nous pouvons par le choix des étoiles, par leur position, et par leur splendeur prendre entre tous les triangles celui qui paraitra le plus propre à l'observation.
Pour parvenir maintenant à la connaissance des longitudes, il faut deux choses : l'une qu'on observe sur mer avec assez d'exactitude le triangle formé par la lune et par les étoiles ; l'autre qu'on connaisse assez exactement le mouvement de la lune pour savoir quelle heure marquerait la pendule réglée dans le lieu où l'on est parti, lorsque la lune forme avec les deux étoiles le triangle tel qu'on l'observe. On peut faire l'observation assez exactement, parce qu'on a assez exactement sur mer l'heure du lieu où l'on est, et que d'ailleurs on a depuis quelques années un instrument avec lequel on peut, malgré l'agitation du vaisseau, prendre les angles entre la lune et les étoiles avec une justesse assez grande pour déterminer le triangle dont nous parlons. La difficulté se réduit à la théorie de la lune, à connaître assez exactement ses distances et ses mouvements pour pouvoir calculer à chaque instant sa position dans le ciel, et déterminer à quel instant pour tel ou tel lieu le triangle qu'elle forme avec deux étoiles fixes, sera tel ou tel. Nous ne dissimulerons point que c'est en ceci que consiste la plus grande difficulté. Cet astre qui a été donné à la terre pour satellite, et qui semble lui promettre les plus grandes utilités, échappe aux usages que nous en voudrions faire, par les irrégularités de son cours : cependant si on pense aux progrès qu'a faits depuis quelque temps la théorie de la lune, on ne saurait s'empêcher de croire que le temps est proche où cet astre qui domine sur la mer, et qui en cause le flux et reflux, enseignera aux navigateurs à s'y conduire, Préface du traité de la parallaxe de la lune par M. de Maupertuis. On verra à l'article LUNE le détail des travaux des plus habiles géomètres et astronomes sur une matière aussi importante.
Il faut avouer que cette méthode pour découvrir les longitudes demandera plus de science et de soin qu'il n'en eut fallu, si on eut pu trouver des horloges qui conservassent sur mer l'égalité de leur mouvement ; mais ce sera aux Mathématiciens à se charger de la peine des calculs ; pourvu qu'on ait les éléments sur lesquels la méthode est fondée, on pourra par des tables ou des instruments, réduire à une grande facilité la pratique d'une théorie difficile.
Cependant la prudence voudra qu'au commencement on ne fasse qu'un usage fort circonspect de ces instruments ou de ces tables, et qu'en s'en servant on ne néglige aucune des autres pratiques par lesquelles on estime la longitude sur mer ; un long usage en fera connaître la sûreté.
Comme les lieux de la lune sont différents pour les différents points de la surface de la terre, à cause de la parallaxe de cette planète, il sera nécessaire dans les observations qu'on fera des lieux de la lune, de pouvoir réduire ces lieux les uns aux autres, ou au lieu de la lune vue du centre de la terre. M. de Maupertuis dans son Discours sur la parallaxe de la lune, dont nous avons tiré une partie de ce qui précéde, donne des méthodes très-élégantes pour cela, et plus exactes qu'aucune de celles qu'on avait publiées jusqu'à lui. Voyez PARALLAXE.
4°. On préfère généralement dans la recherche des longitudes sur terre les observations des satellites de Jupiter à celles de la lune, parce que les premières sont moins sujettes à la parallaxe que les autres, et que de plus elles peuvent toujours se faire commodément quelle que soit la situation de Jupiter sur l'horizon. Les mouvements des satellites sont prompts et doivent se calculer pour chaque heure : or pour découvrir la longitude au moyen de ces satellites, vous observerez avec un bon télescope la conjonction de deux d'entr'eux ou de l'un d'eux avec Jupiter, ou quelques autres apparences semblables, et vous trouverez en même temps l'heure et la minute pour l'observation de la hauteur méridienne de quelques étoiles. Consultant ensuite les tables des satellites, vous observerez l'heure et la minute à laquelle cette apparence doit arriver au méridien du lieu pour lequel les tables sont calculées, et la différence du temps vous redonnera, comme ci-dessus, la longitude. Voyez SATELLITES.
Cette méthode de déterminer les longitudes sur terre est aussi exacte qu'on le puisse désirer, et depuis la découverte des satellites de Jupiter, la Géographie a fait de très-grands progrès par cette raison ; mais il n'est pas possible de s'en servir par mer. La longueur des lunettes jusqu'ici necessaires pour pouvoir observer les immersions et les émersions des satellites, et la petitesse du champ de leur vision, font qu'à la moindre agitation du vaisseau l'on perd de vue le satellite, supposé qu'on l'ait pu trouver. L'observation des éclipses de lune est plus praticable sur mer ; mais elle est beaucoup moins bonne pour connaître les longitudes, à cause de l'incertitude du temps précis auquel l'éclipse commence ou finit, ou se trouve à son milieu ; ce qui produit nécessairement de l'incertitude dans le calcul de la longitude qui en résulte.
Les méthodes qui ont pour fondement des observations de phénomène céleste ayant toutes ce défaut qu'elles ne peuvent être toujours d'usage, parce que les observations ne se peuvent pas faire en tous temps, et étant outre cela d'une pratique difficîle en mer, par rapport au mouvement du vaisseau ; il y a par cette raison des mathématiciens qui ont abandonné les moyens que peuvent fournir la lune et les satellites ; ils ont recours aux horloges et autres instruments de cette espèce, et il faut avouer que s'ils pouvaient en faire d'assez justes et d'assez parfaits pour qu'ils allassent précisément sur le soleil sans avancer ni retarder, et sans que d'ailleurs la chaleur ou le froid, l'air, et les differents climats n'y apportassent aucune altération, on aurait en ce cas la longitude avec toute l'exactitude imaginable ; car il n'y aurait qu'à mettre sa pendule ou son horloge sur le soleil au moment du départ, et lorsqu'on voudrait avoir la longitude d'un lieu, il ne s'agirait plus que d'examiner au ciel l'heure et la minute qu'il est ; ce qui se fait la nuit au moyen des étoiles, et le jour au moyen du soleil : la différence entre le temps ainsi observé, et celui de la machine, donnerait évidemment la longitude. Mais on n'a point découvert jusqu'aujourd'hui de pareille machine ; c'est pourquoi on a eu encore recours à d'autres méthodes.
M. Whiston a imaginé une méthode de trouver les longitudes par la flamme et le bruit des grands canons. Le son, comme on le sait, se meut assez uniformément dans toutes ses ondulations, quel que soit le corps sonore d'où il part, et le milieu par où il se transmet. Si l'on tire donc un mortier ou un grand canon dans un endroit où la longitude est connue, la différence entre le temps où le feu, qui se meut comme dans un instant, sera vu, et celui où le son qui se meut sur le pied de 173 taises par seconde, sera entendu, donnera la distance des deux lieux l'un de l'autre ; ainsi en supposant qu'on eut la latitude des lieux, on pourra par ce moyen parvenir à la connaissance de la longitude. Voyez SON, etc.
De plus si l'heure et la minute où l'on tire le canon sont connues pour le lieu où l'on le tire, observant alors, par le soleil et les étoiles, l'heure et la minute dans le lieu dont on cherche la longitude, et où nous supposons qu'on entend le canon même sans le voir, la différence de ces deux temps sera la différence de longitude.
Enfin, si ce mortier était chargé d'un boulet creux ou d'une manière de bombe pleine de marière combustible, et qu'on le plaçât perpendiculairement, il porterait sa charge à un mille de haut, et on en pourrait voir le feu à près de cent milles de distance. Si l'on se trouve donc dans un endroit d'où l'on ne puisse apercevoir la flamme du canon, ni en entendre le son, on pourra néanmoins déterminer la distance du lieu où on sera, à celui où le mortier aura été braqué, par la hauteur dont la bombe s'élevera au-dessus de l'horizon : or la distance et la latitude étant une fois connues, la longitude se trouvera facilement.
Suivant cette idée, on proposait d'avoir de ces mortiers placés de distance en distance, et à des stations connues, dans toutes les côtes, les iles, les caps, etc. qui sont fréquentés, et de les tirer à certains moments marqués de la journée pour l'usage et l'avantage des navigateurs.
Cette méthode, qui pourrait plaire à l'esprit dans la théorie est cependant entièrement inutile, parce qu'elle est très-incommode et même qu'elle suppose trop. Elle suppose, par exemple, que le son peut-être entendu de 40, 50 ou 60 milles, et il est vrai qu'on en a des exemples ; mais ces exemples sont très-rares, et d'ordinaire le bruit du canon ne s'entend que de la moitié au plus de cet espace, et quelquefois de beaucoup moins loin. Elle suppose encore que le son se meut toujours avec une egale vitesse, au lieu que dans le fait sa vitesse peut augmenter ou diminuer selon qu'il se meut ou en même sens que le vent, ou en sens contraire.
Il est vrai que suivant quelques expériences le vent n'altère en rien la vitesse du son ; mais ces expériences auraient besoin d'être répétées un grand nombre de fois pour qu'on put en déduire des règles générales ; et il y en a même qui leur paraissent contraires, puisque souvent on entend les cloches lorsque le vent en pousse le son aux oreilles, et qu'on cesse de les entendre quand le vent y est contraire.
Cette méthode suppose enfin que la force de la poudre est uniforme, et que la même quantité porte toujours le même boulet à la même hauteur ; or il n'y a aucun canonnier qui ne sache le contraire. Nous ne disons rien des nuits couvertes et obscures où on ne peut point voir de lunes, ni des nuits orageuses ou on ne peut point entendre le son, même à de très-petites distances.
C'est pourquoi les marins sont réduits à des méthodes fort imparfaites pour trouver la longitude : voici une idée générale de la principale de ces méthodes. Ils estiment le chemin que le vaisseau a fait depuis l'endroit d'où ils veulent compter la longitude, ce qui ne se peut faire que par des instruments jusqu'ici fort peu exacts. Ils observent la latitude du lieu où le vaisseau est arrivé, et la comparant à la latitude de l'autre lieu pour savoir combien ils ont changé en latitude ; et connaissant à-peu-près le rhumb de vent sous lequel ils ont couru pendant ce temps, ils déterminent par la combinaison de ces différents éléments la différence des longitudes.
On voit assez combien d'éléments suspects entrent dans cette détermination, et combien la recherche des longitudes à cet égard est encore loin de la perfection qu'on y désire.
On peut encore se servir de la déclinaison de la boussole pour déterminer la longitude en mer. Voyez sur cela le Traité de navigation de M. Bouguer, pag. 313, ainsi que les méthodes les plus usitées par les marins pour trouver la longitude. (O)
LONGITUDE
- Détails
- Écrit par Jean le Rond d'Alembert (O)
- Catégorie parente: Science
- Catégorie : Astronomie
- Affichages : 2170